

















2.10 Division of Polynomials
We have learnt the
following statement to be true for any number
Dividend = (divisor*quotient) + remainder.
The above relationship holds good for polynomials
also.
2.10.1
Division of Monomial by monomial
2.10.1 Problem 1: Divide 12m3 n5 by 4 m2 n
Solution:
Step 1: 12m3 n5 / 4 m2 n
= (12/4)* (m3
n5 /m2 n)
Step 2:
12/4 = 3,
Step 3:
m3 n5/ m2 n = m3-2
n5-1 = m n4
![]() 12m3 n5 /4 m2 n = 3 m n4
12m3 n5 /4 m2 n = 3 m n4
Verification:
Divisor*quotient +
reminder = 4 m2 n*3 m n4 +0 =12 m2+1
n1+4 =12m3 n5 which is dividend
2.10.1 Problem 2 : Divide 57x2y2z2 by 19xyz
Step 1 :
57x2y2z2 /19xyz = (57/19) * (x2y2z2)/xyz
Step 2:
57/19 =3
Step 3:
x2y2z2/xyz = x2-1y2-1z2-1
= xyz
Thus 57x2y2z2
/19xyz =
(57/19) * (x2y2z2)/xyz =3xyz
Verification:
(Divisor*Quotient) + Remainder = (3xyz * 19xyz) +0
= (3*19)*xyz*xyz +0= 57x1+1y1+1z1+1+0=57x2y2z2 which is dividend!
We observe 3 is quotient of 57/19 which is nothing
but quotient of coefficients of monomials (57 and 19)
Similarly xyz is quotient of x2y2z2
/xyz which is nothing but quotient of the variables (x2y2z2
and xyz)
Steps to divide a monomial by monomial:
The quotient has two
parts coefficient and variable. How do we get these?
1. The coefficient of quotient of two monomials is
equal to the quotient of their coefficients
2. The variable part in the quotient of two
monomials is nothing but the quotient of the variables in the monomials
2.10.2 Division of a
Polynomial by a Monomial
2.10.2 Problem 1: Divide 4023m2n2-6032m2n
-8042m3 n4 by (-2012m2)
Solution:
We know that
4023= (2x201)3=
(2)3x(201)3, 6032 = (3x201)2 = (3)2x(201)2,
8042 = (4x201)2 =
(4)2x(201)2
![]() [4023m2n2-6032m2n
-8042m3 n4]/(-2012m2)
[4023m2n2-6032m2n
-8042m3 n4]/(-2012m2)
=[(2)3*(201)3
m2n2-(3)2*(201)2 m2n
-(4)2*(201)2m3 n4]/(-2012m2)
= -[ (2)3*(201) n2-(3)2*
n -(4)2*m1 n4] = -
(8*201* n2-9n -16mn4)
Verification:
Divisor*quotient +
reminder
= (-2012m2)*[-(8*201* n2+9n
+16mn4)]+0=
= +(2012m2)*(8*201*
n2 -2012m2*9n -2012m2*16mn4)
+0
= 8*2013m2 n2
-9*2012m2+2n-16*2012m2+1n4)
= 23* 2013m2 n2 - 32 *2012m4n-42*2012
m3 n4
= (2*201)3m2n2-(3*201)2
m2n (4*201)2 m3 n4
= 4023 m2n2 - 6032
m2n - 8042 m3 n4
= dividend
2.10.2 Problem 2 : Divide 2a4 b3+ 8a2
b2 by 2ab
Solution:
(2a4 b3+
8a2 b2)/2ab = (2a4 b3/2ab) + (8a2
b2 / 2ab) = a3 b2 +4a b
Verification:
Divisor*quotient +
reminder = 2ab*(a3 b2 +4a b) +0= 2a4 b3+
8a2 b2 which is dividend
Steps to divide a polynomial by the monomial:
1. Divide each term of
the polynomial by the monomial.
2. The partial quotients when expressed
collectively become the quotient of polynomial.
2.10.3
Division of a Polynomial by a Binomial/Trinomial (Long division method)
2.10.3 Problem 1: To begin with let us
learn the steps of division by dividing 7+x3-6x (a trinomial) by
x+1(a binomial)
Solution:
Note degree of dividend(x3 -6x+7) is 2 and degree of divisor(x+1) is 1
|
Step |
Procedure |
|
|
1 |
Arrange the terms of dividend and divisor in
descending order of their degrees(Already in descending order) |
|
|
2 |
If
any term of a degree is missing in dividend or divisor, add that degree with
coefficient as 0. Write
dividend x3 -6x+7
as x3 +0x2-6x+7 |
|
|
3 |
Divide
the first term of the dividend by the first term of the divisor,( x3/x
= x2) Hence, x2 is
the first term of the quotient, write this term on the top of the dividend. |
|
|
4 |
Multiply
divisor(which is x+1) by the first term of the quotient(which is x2)
and write the
product(=x3+ x2)
below the dividend |
|
|
5 |
Subtract
result of step 4 from the given dividend. The result is ( x3 +0x2
) (x3+ x2) = - x2 |
|
|
6
|
Take
term of next degree (=-6x) from the
given dividend and write it next to the result got in step 5. The
result is -x2 6x. Consider this as new dividend |
|
|
7
|
Repeat
steps 3 to 6, by taking terms from given dividend in step corresponding to step 6 |
|
|
8 |
Repeat
above procedure till the degree of reminder is less than degree of divisor |
Verification:
Divisor *Quotient +Reminder = (x+1)* (x2-x-5)+12 = x*(x2-x-5) +1*(x2-x-5)+12
= (x3-x2-5x)+ (x2-x-5)+12 = x3-x2+
x2-5x-x -5+12 = x3-0x2-6x +7 = x3-6x
+7
which is nothing but
dividend
2.10.3 Problem 2: x5 -9x2 +12x-14 divided by x
-3
Solution:
Though, the dividend is in descending order of
power of x, we need to have missing terms of powers of x (x4
,x3). This is done by having their co-efficients as
zero.
The dividend is re written as x5 +0x4 +0x3-9x2
+12x-14. The divisor is already in descending order of power of x.
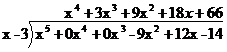
- | x5 -3x4
- |3x4
+0x3
- |3x4 -9x3
- |9x3
-9x2
- |9x3
-27x2
- |18x2+12x
- |18x2 -54x
-|66x-14
-|66x-198
184
Verification:
We can verify the solution by doing proper
multiplication of terms.
Since terms are big, let us verify by an
alternative method of substitution.
Let us find the results when x=2
Then
Dividend =x5 -9x2 +12x-14 = 25
-9*22 +12*2-14 = 32-36+24-14 = 6
Divisor = x-3 =2-3 = -1
Quotient = ![]() = 24 +3*23
+9*22+18*2+66 = 16+24+36+66=178
= 24 +3*23
+9*22+18*2+66 = 16+24+36+66=178
Quotient*Divisor + Reminder = 178*-1+184 =
-178+184= 6 which is dividend
2.10.3 Problem 3: Divide 6p3 -19p2
-8p by p2 -4p+2
Solution:
6p+5
p2 -4p+2![]()
( -) |6p3 -24p2 +12p --ΰ ---- (1) {= 6p*(p2 -4p+2)}
(=) |+5 p2 -20p --ΰ -----(2) {subtract (1) from given dividend}
( -) | 5p2 - 20p+10 --ΰ -----(3) {= 5*(p2 -4p+2)}
(=) -10
--ΰ {subtract (3) from (2)}
Verification:
Quotient *Divisor
= (6p+5)* (p2
-4p+2) = 6p* p2
+6p*-4p+6p*2+5* p2+5*-4p+5*2 = 6p3
-24p2+12p+5p2-20p+10
=6p3 -19p2-8p+10
Quotient *Divisor + Reminder = (6p3
-19p2-8p+10)-10 = 6p3
-19p2-8p which is dividend
2.10.3 Problem 4: Divide a5
+b5 by a+b
Solution:
a+b
(-) |a5+ a4b
(=) - a4b+0
(-) |a4b-a3b2
(=) a3b2+0
(-) | a3b2+ a2b3
(=)
- a2b3+0
(-)
|-a2b3-ab4
(=)
ab4 + b5
(-) |ab4 + b5
(=) 0
Exercise : Verify that Divisor*Quotient+ Reminder = dividend
2.10 Summary of
learning
|
No |
Points studied |
|
1 |
Division
of algebraic expressions |
Additional points:
Synthetic method (Horners method) of division when the divisor
is of the form x-a.
We shall describe this method by taking the problem
which was worked out earlier (2.10.3 Problem 2).
Divide x5 -9x2
+12x-14 by x -3
Solution:
Write the dividend in its standard form as: 1x5 + 0x4 + 0x3 - 9x2 + 12x - 14.
Here the constant term in the divisor is -3
First, write the negative of constant term in the
divisor (3 in this case)
in the first column of
the first row. In
the next columns of the first
row write the co-efficients of the dividend (1,
0, 0, -9, 12, -14)
Write the co-efficient of the first term of the divisor
(in this case 1) in the corresponding column of the third row down below (in 2nd
column).
starting from this column in
the third row, write the product of divisor (in this case 3) and the number in
this column (in this case 1) in the next column of 2nd row (in this
case 3*1=3 in the 3rd
column). Add these numbers in the 1st and 2nd row (in
this case 0+3=3) into the corresponding column in the third row. Repeat this
process till the result in the last column in the third row is got. The value
in the last column of the third row gives the reminder.
|
Divisor |
Dividend portion |
|
|||||
|
3 |
1 |
0 |
0 |
-9 |
12 |
-14 |
First Row |
|
|
|
3(=3*1) |
9(= 3*3) |
27(= 3*9) |
54(= 3*18) |
198(= 3*66) |
Second
row |
|
|
1 |
3=(0+3) |
9(= 0+9) |
18(=-9+27) |
66(=12+54) |
184(=-14+198) |
Third
row |
You will observe that the reminder is
184, which is same as what we got while solving problem (2.10.3 Problem 2)
Roots of
an equation:
Let us take the polynomial 4023m2n2
- 6032m2n - 8042m3 n4.
Since this polynomial contains m and n as variables
we can denote the same by f(m,n).
f(m,n) is pronounced as function of m and n.
f(m,n) = 4023m2n2
- 6032m2n - 8042m3 n4
A polynomial f(x) in one variable x is an algebraic
expression of the form
f(x) = anxn+ an-1xn-1+
an-2xn-2+
. a2x2+ a1x+
a0 = 0
where a0,a1,a2,
an-1,an are constants and an ![]() 0
0
a0,a1,a2,
an-1
and an are called co-efficients
of x0,x1,x2
.
xn-1 and xn respectively. n is
called the degree of the polynomial.
Each of anxn, an-1xn-1,
. a2x2,
a1x1, a0 are called the terms of the polynomial.
Let f(x) = x5 - 9x2 + 12x - 14
If we substitute x = 0 we get f(0)
= 0 -9*0 +12*0 -14 = -14
If we substitute x = 1 we get f(1)
= 1-9+12-14= -10
Similarly, if we substitute x = -1 we get f(-1) = -36
f(a) = a5 - 9a2
+ 12a - 14
If for any value of a (x=a), f(x) = 0, then we say
that a is a root of the equation f(x)=0.
2.10.3 Problem 5: Check if 0, 1, 2 are roots of the equation x2-2x=0
Solution:
Let f(x) = x2-2x
We note that f(0) = 02-2*0
= 0,
f(1) = 12-2 = -1
f(2) = 22-2*2 = 0
Thus 0 and 2 are the roots of the given polynomial
but 1 is not.
2.10.3 Problem 6: If f(x) = x2+5x+p and q(x) = x2+3x+q
have a common factor then
(i) Find the common factor
(ii) Show that (p-q)2=
2(3p-5q)
Solution:
Since degree of f(x) is 2 and it has a common factor,
the degree of the factor has to be one.
Let it be x-k
![]() f(k)
= k2+5k+p = 0
f(k)
= k2+5k+p = 0
Since x-k is also a factor of q(x)
![]() q(k)
= k2+3k+q = 0
q(k)
= k2+3k+q = 0
![]() k2+5k+p = k2+3k+q: On simplification
k2+5k+p = k2+3k+q: On simplification
![]() k = (1/2)(q-p)
k = (1/2)(q-p)
Hence the common factor = x-k = x - (1/2)(q-p)
= x + (1/2)(p-q)
By substituting the value of k in f(x) we get
((q-p)/2)2+5(q-p)/2+p = 0
i.e. (p-q)2/4+5(q-p)/2+p
= 0
i.e. (p-q)2+10(q-p)+4p
= 0
i.e. (p-q)2
= 10p-10q-4p
= 6p-10q
= 2(3p-5q)








