6.8 Parallelogram:

6.8.1 Construction of parallelogram

We have seen earlier (6.7.1) that to construct unique quadrilaterals, we require five elements - a suitable combination of sides, diagonals

and angles as given below

No.	No of sides given	Number of diagonals given	Number of angles given	Total Number of elements required
1	2	2	1	5
2	2	1	2	5
3	4	1	-	5
4	4	-	1	5
5	3	-	2(Included)	5
6	3	2	-	5
7	2(Adjacent)	-	3	5

Since parallelogram has a special property of opposite sides being parallel and opposite angles being equal,

we just need three elements to construct a unique parallelogram as given below

No.	No of sides given	Number of diagonal given	Number of angles given	Total Number of elements required
1	2	1	-	3
2	2	-	1	3
3	-	2	1(Intersecting )	3
4	1	2	-	3

6.8.1.1 Construction of a parallelogram given the length of 2 adjacent sides and a diagonal.

In a parallelogram, opposite sides are equal. If lengths of 2 adjacent sides are given, we can arrive at the lengths of all sides.

Thus, the construction is similar to that of a quadrilateral with 4 sides and 1 diagonal given (Refer 6.6.1).

6.8.1 Exercise 1: Construct a parallelogram whose adjacent sides are 5cm and 3cm and diagonal is 6cm.

(The sides are 5cm, 3cm, 5cm and 3cm and diagonal is 6cm)

6.8.1.2. Construction of a parallelogram given the length of 2 adjacent sides and an angle.

In a parallelogram, opposite sides are equal. If lengths of 2 adjacent sides are given, we can arrive at the lengths of all sides.

Thus, the construction is similar to that of a quadrilateral with 4 sides and 1 angle given (Refer 6.6.1).

6.8.1 Exercise 2: Construct a parallelogram PQRS, given PQ=5cm, QR=4cm and PQR = 70⁰.

(The sides are PQ=5cm, QR=4cm, RS=5cm and PS=4cm and PQR = 70⁰)

6.8.1.3. Construction of a parallelogram given the length of two diagonals and intersecting angles between them.

6.8.1 Problem 1: Construct a parallelogram whose diagonals are 4cm and 5cm and the angle between them is = 70⁰.

First draw a rough diagram of ABCD with AC and BD as diagonals.

Step	Construction
1	Mark a point A and draw a line though A
2	From A, draw an arc of radius 4cm to cut the above line at C (AC=4cm)
3	Bisect AC at O (From A and C, draw arcs of radius more than half the length of AC on both sides, Let they cut at X and Y. XY is the perpendicular bisector of AC. It cuts AC at O
4	From O, draw a line at an angle 70⁰ to AC on both sides
5	From O, draw an arc of radius 2.5cm on both sides of AC to cut the above line at B and D. Join AB, BC, CD and DA.

ABCD is the required parallelogram.

6.8.1.4. Construction of a parallelogram given the length of one side and two diagonals.

With the given side as the base, construct a triangle (with half of diagonals as other two sides) by using the property that diagonals of a

parallelogram bisects each other. Then extend these other two sides.

6.8.1 Exercise 3: Construct a parallelogram ABCD with BC=4.5cm and diagonals AC=4cm and BD=5.0cm.

In the figure of 6.8.1 Problem 1 use the property AO=OC and BO=OD to construct triangle BCO with BC= 4.5cm, CO=2cm and BO=2.5cm and then extend CO and BO such that OA = 2cm and OD=2.5cm. Join CD,DA,AB

6.8.1.5. Construction of a parallelogram given the length of adjacent sides and the height of parallelogram.

6.8.1 Exercise 4: Construct a parallelogram ABCD, with adjacent sides AB=4 cm, BC = 5cm and height corresponding to BC =3.5 cm

Step	Construction
1	Mark a point B and draw a line though B
2	From B, draw an arc of radius 5cm to cut the above line at C (Hence BC=5cm)
3	Draw 2 perpendicular lines XY and PQ on BC at any two points U and T on it.
4	From U and T cut PQ and XY at S and R by an arc of radius 3.5 cm Join RS ( Note RS is at a distance of 3.5cm from BC)
5	Cut the line RS at A by an arc of radius 4cm from B (Hence BA=4cm)
6	From A cut the line RS at D by an arc of radius 5cm ( Hence AD=5cm)

ABCD is the required parallelogram.

6.8.2 Area of parallelogram

ABCD is a parallelogram with AB||CD, BC||AD and AB=CD, AD=BC.

From D and C draw perpendiculars to AB (extend if necessary). Let them meet AB at E and F.

DE and CF are the altitudes of the parallelogram. Since AB||CD, altitudes are equal (DE=CF).

The triangles ADE and BFC are congruent triangles

(AD=BC, DE=CF and DEA = BFC =90⁰ – SAS Postulate)

and hence AE=BF and hence Area of ADE = Area of BFC.

Area of ABCD = Area of ADE + Area of quadrilateral DEBC

= Area of BFC + Area of quadrilateral DEBC = Area of rectangle DEFC = Length * breadth

= DC * h

Area of the parallelogram = base*height

6.8.2 Problem 1: ABCD is a parallelogram with AB=24cm and AD=16cm. The distance between AB and DC is 10cm. Find the distance between AD and BC.

Solution:

The distance between AB and DC is the height (DE).

Area of the parallelogram ABCD = base*height = 24*10 = 240sq cm

This is also the area of the same parallelogram with AD as the base and AH as the height.

Area of ABCD = AD*AH = 16*AH

But area = 240sqcm

16*AH = 240

I.e. AH = 240/16 = 15cm

6.8.2 Problem 2: A rectangle and a parallelogram have equal areas. The sides of the rectangle are 10m and 14m.

The base of the parallelogram is 20m. What is the altitude of the parallelogram?

Solution:

We know that the Area of rectangle = side*side = 10*14 = 140sqm

Area of parallelogram = Base*Altitude = 20*Altitude

Since both the areas are same

Area of parallelogram =140sqm

20*Altitude = 140

i.e. Altitude = 140/20 = 7mts

6.8.2 Problem 3: A triangle and a parallelogram have equal areas and equal bases. What is the ratio of their altitudes?

Solution:

If B_P and H_P are base and altitude of the parallelogram, then the

area of parallelogram = Base *Altitude = B_p*H_p

If B_T and H_T are base and altitude of the triangle, then the area of triangle

= 1/2(Base *Altitude) = 1/2(B_T*H_T).

Since the areas are same, B_p*H_p=1/2(B_T*H_T).

Since the bases are same, B_P= B_T.

We have

H_p=1/2H_T

i.e. 2H_p=H_T

Therefore the altitude of the triangle is twice the altitude of the parallelogram.

6.8.2 Problem 3: Have you observed your mother, grandmother or those who make sweets cutting .Burfis in the shape of parallelogram than rectangles?

(Did they study geometry?)

For example let the sides of rectangle and parallelogram be 13 and 12 units.

Area of rectangle = base * another side = 12*13= 156 square units

Area of parallelogram = base * height = 12*12= 154 square units

( we used the pythogoras theorem to find the height of parallelogram

(12²= 13²-5²)

Thus we notice that area of parallelogram < area of rectangle

Though the sides of rectangle and parallelogram are same, area of rectangle is more than the area of parallelogram. Hence in the same spread (area)

they can cut more number of pieces in the shape of parallelograms than in the shape of rectangles.

6.8.3 Construction of Rhombus:

We have seen that, to construct a parallelogram we need three elements (suitable combination of sides, diagonals and angles).

Because of the special property of rhombus, only two elements are enough to construct a rhombus uniquely.

1. Length of two diagonals are given .

6.8.3 Problem 1: Construct a rhombus PQRS with PR = 5cm and SQ=4cm

First draw a rough diagram

Step	Construction
1	Mark a point P and draw a line though P
2	Draw an arc of radius 5cm to cut the above line at R (PR=5cm)
3	Bisect PR at O (From P and R, draw arcs of radius more than half the length of PR, on both sides of PR. Let they cut at X and Y. (XY is the perpendicular bisector of PR)
4	From O draw an arc of radius 2cm to cut OX at S(OS=2cm)
5	From O draw an arc of radius 2cm to cut OY at Q(OQ=2cm). Join PQ, QR, RS and SP.

PQRS is the required rhombus.

2. Lengths of one side and one diagonal are given

6.8.3 Problem 2: Construct a rhombus ABCD with AB = 3cm and AC=4cm

First draw a rough diagram

Step	Construction
1	Mark a point A and draw a line though A
2	Draw an arc of radius 4cm to cut the above line at C (AC=4cm)
3	From A, draw arcs of radius 3cm on both sides of AC
4	From C, draw arcs of radius 3cm on both sides of AC to cut the above arcs at D and B. Join AB, BC, CD and DA.

ABCD is the required rhombus

3. Lengths of one side and one angle are given

6.8.3 Problem 3: Construct a rhombus ABCD with AB = 3cm and ABC = 120⁰.

First draw a rough diagram

Step	Construction
1	Mark a point B and draw a line though B
2	Draw a line through B at an angle of 120⁰ with BC
3	From B, draw an arc of radius 3cm to cut the above line at A (BA=3cm and ABC = 120⁰)
4	From A and C, draw arcs of radius 3cm to meet at D. Join AD and DC.

ABCD is the required rhombus

6.8.4 Area of Rhombus:

We have seen(in 6.6) that a diagonal of a rhombus cuts the rhombus into 2 congruent triangles.

We shall use this property to calculate the area of rhombus, as we already know how to

calculate the area of a triangle.

In the rhombus PQRS, draw the diagonal PR and QS.

As PQRS is a rhombus, diagonals bisect each other perpendicularly (SOR = ROQ = 90⁰)

OS and OQ are the altitudes of PRS and PRQ

Area of PRS= ½(base*height) =1/2(PR*OS)

Area of PRQ = ½(base*height) = 1/2(PR*OQ)

Area of PQRS = Area of PRS + Area of PRQ

= 1/2(PR*OS) + 1/2(PR*OQ) = 1/2*PR* (OS+OQ) =1/2*PR*QS sq units

Area of a rhombus = ½ * product of diagonals

Note : This formula was also given by Bhaskracharya (Lilaviti Shloka 176).

6.8.4 Problem 1: The longer diagonal of a rhombus is greater than the other diagonal by 10mts. The sum of diagonals is 32mts. Find its area.

Solution:

Let the shorter diagonal be x.

Since the longer diagonal is greater than the other diagonal by 10mts, its length will be x+10.

Since the sum of diagonals is 32m.

We have

x+(x+10) = 32

i.e. 2x+10 =32

i.e. 2x=32-10 =22

x=11mts

Hence its diagonals are 11 and 21(=11+10) meters.

We know that

Area of a rhombus = 1/2 * product of diagonals = 1/2*11*21 = 231/2 sq mts

6.8.4 Problem 2: The perimeter of a rhombus is 40cm and one of its diagonal is 16cm. Find the other diagonal and area of rhombus.

Solution:

Let x be the side. Since perimeter is sum of all sides and all sides are equal in a rhombus:

We have 4x = 40cm

x=10cm

Thus in PQRS PQ = 10cm.

As PQRS is a rhombus, diagonals bisect each other perpendicularly (PO=OR and QO=OS).

PR=16cm(given)

PO=OR=8cm

POQ is a right angled triangle with PQ=10 and PO=8

By Pythagoras theorem

PQ²= PO²+OQ²

OQ² =PQ²-PO² = 10²-8² = 100-64 =36= 6² OQ = 6

Since OQ=OS, we have OS=6cm and hence QS =6+6=12cm

Area = 1/2* product of diagonals = 1/2* 16*12= 96 sq cms

6.8.5 Construction of Trapezium:

Trapezium can be thought of as a figure got by merging a triangle with parallelogram.

We have seen that to construct a quadrilateral we require five elements. Since trapezium has one pair of opposite sides parallel,

we require a maximum of four elements to construct a trapezium uniquely.

6.8.5.1. When length of two sides and two angles are given

6.8.5 Problem 1: Construct a trapezium ABCD with AB||CD, AB=5cm, CD=3cm and (DAB = 70⁰ ABC = 50⁰)

First draw a rough diagram.

Step	Construction
1	Mark a point A and draw a line though A
2	From A, draw an arc of radius 5cm to cut the above line at B (AB=5cm)
3	From A, draw an arc of radius 2cm (=AB-CD) to cut AB at E (AE=2cm)
4	Draw a line through A at an angle of 70⁰ to AB
5	Draw a line through E at an angle of 50⁰ to AB to cut the above line at D
6	Draw a line through B at an angle of 50⁰ to AB.
7	From D, draw an arc of radius 3cm to cut the above line at C (DC=3cm and ABC = 50⁰). Join DC.

ABCD is the required trapezium.

Note: In step 4, we used the property of corresponding angles being equal when a transversal cuts two parallel lines (Here DE cuts AB and CD).

6.8.5. 2. When lengths of parallel sides and the altitude are given.

6.8.5 Problem 2: Construct a trapezium PQRS with PQ||SR, PQ=5cm, SR=6cm and PS=3cm

First draw a rough diagram.

Step	Construction
1	Mark a point P and draw a line though P
2	From P, draw an arc of radius 5cm to cut the above line at Q (PQ=5cm)
3	Draw a perpendicular from P (altitudes form 90⁰)
4	From P, draw an arc of radius 3cm to cut the above line at S (PS=3cm)
5	Draw a perpendicular from S (parallel to PQ)
6	From S, draw an arc of radius 6cm to cut the above line at R (SR=6cm)

6.8.5. 3. When lengths of all sides are given.

Since trapezium can be thought of as consisting of a triangle and Parallelogram first construct a triangle of three sides like what is explained in 6.8.5 Problem1.

6.8.5 Exercise 1: Construct a trapezium ABCD with AB||CD, AB=7cm, DC=5cm, AD=2cm and BC= 2.5cm

Hint: Draw a rough diagram as in the figure on the right side. Mark E on AB such that AE=AB-CD

Construct triangle AED such that AD =2cm, DE =BC=2.5cm

From B draw a line parallel to ED and mark C such that BC=2.5cm, Join D and C

ABCD is the required trapezium

6.8.5 Problem 3: Construct an isosceles trapezium ABCD with CD||AB, AB=7cm, AD=2cm and DC=5cm

Since in an isosceles trapezium non parallel sides are equal, we have BC=AD.

Thus, we have to construct a trapezium ABCD with four sides given

(DA=2cm, AB=7cm, BC=2cm and CD=5cm).

Hint: As in 6.6.8 Problem 1, first we need to construct a triangle AED with AE = AB-DC = 7-5 = 3cm

1. With AD=2cm (given), AE = 3cm (construction) and DE = CB = 2cm (parallelogram), we should be able to construct the triangle ADE.

2. From B, draw an arc of radius 2cm and from D draw an arc of radius 5cm to cut at point C. Join DC and CB.

3. ABCD is the isosceles trapezium.

6.8.6 Area of Trapezium:

ABCD is a trapezium with BC||AD and AB=CD.

Draw perpendiculars from A and D to the base BC to cut BC at E and F respectively.

Since BC and AD are parallel, the altitudes AE and DF are equal (the distance between parallel lines are always same)

Note that AEFD is a rectangle. Therefore EF =AD and hence EF = 1/2EF+1/2EF=1/2(EF+AD)

Area of trapezium ABCD = Area of ABE + Area of rectangle AEFD+ Area of DFC

= 1/2(base*height)+ (side*side)+ 1/2(base*height)

= 1/2(BE*height)+ (EF*height)+ 1/2(FC*height)

= (BE/2 + EF + FC/2)*height

= (BE/2+(EF+AD)/2+FC/2)*height (EF=AD and hence EF = 1/2( EF+AD))

= 1/2(BE+EF+AD+FC)*height

= 1/2(BE+EF+FC+AD)*height = 1/2(BC+AD)*height

Area of trapezium = half the product of height and sum of parallel sides

6.8.6 Problem 1: The parallel sides of a trapezium are in the ratio of 2:1. If the distance between the parallel sides is 6cm and the area is 135 sq cm,

find the length of parallel sides.

Solution:

It is given that the height of the trapezium is 6cm.

Since parallel sides of the trapezium are in the ratio of 2:1, let the sides be 2x and 1x.

We know

Area of trapezium = half the product of height and sum of parallel sides

= 1/2(6*(2x+x)) = 3*3x = 9x

We are also given that the area is 135sq cm 9x=135 x= 15cm: 2x =30cm

The parallel sides of trapezium are 15cms and 30cms.

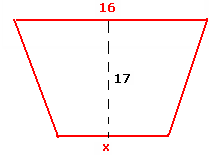
6.8.6 Problem 2: The area of a trapezium is 204sq cm. Its altitude is 17cm and one of the parallel sides is 16cms. Find the other side.

Solution:

Let x be the other side

Area of trapezium = half the product of height and sum of parallel sides

= 1/2(17*(16+x))

We are given that the area is 204 sq cm

1/2(17*(16+x)) =204 i.e. 17 (16+x) =408 i.e. 16+x =408/17 = 24 i.e. x = 24-16= 8cm

The other side is 8cm

Verification

Area of trapezium = 1/2*17*(16+8) = 17*12 = 204 sq cm which is as given in the problem.

6.8.7 Theorems on parallelograms:

6.8.7 Theorem 1: The diagonals of a parallelogram bisect each other.

Data: ABCD is a parallelogram. The diagonals AC and BD meet at O.

To prove: AO=OC and BO=OD

Proof:

Steps	Statement	Reason
1	AB = CD	Opposite sides of parallelogram
2	BAO = OCD	Alternate angles of AB\|\|CD, AC is transversal
3	ABO = ODC	Alternate angles of AB\|\|CD, BD is transversal
4	ABO CDO	ASA Postulate
5	AO=OC and BO=OD	Corresponding sides of congruent triangles

This proves that the diagonal of a parallelogram bisect each other.

6.8.7 Theorem 2: Each diagonal divides a parallelogram in to two congruent triangles.

Data: ABCD is a parallelogram, AC is a diagonal

To prove: ABC ACD

Proof:

Steps	Statement	Reason
1	AB = CD	Opposite sides of parallelogram
2	BC = AD	Opposite sides of parallelogram
3	AC is common
4	ABC ACD	SSS Postulate

This proves that the diagonal divides the parallelogram in to two congruent triangles.

Corollary means a result/effect of a main event.

For example,

August 15^th is celebrated as the independence day of India and is one of the three national holidays; consequently we can say that it is a holiday

for schools/colleges/offices.

The main event here is Independence Day. Corollary to that is, it is a holiday.

Similarly, based on Theorems we derive Corollaries.

6.8.7 Corollary 1: In a parallelogram, if one angle is a right angle then it is a rectangle.

Given: ABCD is a parallelogram. ABC = 90⁰

To Show: ABCD is a rectangle

Steps	Statement	Reason
1	ABC = 90⁰	Given
2	ABC+BCD = 180⁰	Sum of two consecutive angles is 180⁰
3	BCD = 90⁰	Substitution in step 2 for ABC
4	CDA =ABC	Opposite angles of a parallelogram
5	CDA = 90⁰
6	BAD= BCD	Opposite angles of a parallelogram
7	BAD = 90⁰

Hence ABCD is a rectangle

6.8.7 Corollary 2: In a parallelogram, if all the sides are equal and all the angles are equal, then it is a square.

Given: ABCD is a parallelogram and AB=BC=CD=DA.

To Show: ABCD is a square

Steps	Statement	Reason
1	BAD+ADC = 180⁰	Sum of two consecutive angles is 180⁰
2	2BAD = 180⁰	Given that all the angles are equal
3	BAD=ADC=90⁰
4	ABC+BCD = 180⁰	Sum of two consecutive angles is 180⁰
5	2ABC = 180⁰	Given that all the angles are equal
6	ABC=BCD=90⁰
7	All are right angles

Since it is also given that all sides are equal, ABCD is a square.

6.8.7 Corollary 3: The diagonals of a square are equal and bisect each other perpendicularly.

Given: ABCD is a square hence AB=BC=CD=DA and ABC =BCD=CDA=DAC=90⁰

To Show: AC=BD,AO=CO,BO=DO,AOB=BOC = 90

Steps	Statement	Reason
	Consider ABC and BCD
1	AB=CD	In a square, all sides are equal
2	BC is common
3	ABC=BCD = 90⁰	In a square all angles are right angles
4	ABC BCD	SAS Postulate
5	AC=BD	Corresponding sides are equal
	Consider ABO and OCD
6	AB=CD	In a square, all sides are equal
7	ABO =ODC	Alternate angles of AB\|\|CD, BD is transversal
8	BAO=OCD	Alternate angles of AB\|\|CD, AC is transversal
9	ABO OCD	ASA Postulate
10	AO=OC,BO=OD	Corresponding sides are equal
	Consider ABO and OCB
11	AB=BC	In a square, all sides are equal
12	AO=OC	BO bisects AC (Step 9)
13	BO is common
14	ABO OCB	SSS Postulate
15	AOB=BOC	Corresponding angles are equal
16	AOB+BOC=180⁰	Sum of angles on a straight line is 180⁰
17	2AOB=180⁰
18	AOB=90⁰=BOC	(Step 15)

Hence the diagonals of a square bisect each other at right angles.

6.8.7 Corollary 4: The straight line segments joining the extremities of two equal and parallel line segments on the same side are equal and parallel.

Given: AB=CD and AB||DC and A is joined with D and B is joined with C

To Show: AD=BC and AD||BC

Construction: join AC.

Steps	Statement	Reason
1	AB=CD	Given
2	DAC=ACB	Alternate angles of AB\|\|DC, AC is transversal
3	AC is common
4	ABC ACD	SAS Postulate
5	AD=BC	Corresponding sides are equal
6	DAC=ACB	(Step 2)

Since DAC and ACB are alternate angles with respect to the lines AD and BC with AC as a transversal, AD||BC.

6.8.7 Problem 1: In the adjoining adjacent figure, ABCD is a parallelogram. P is the mid point of BC. Prove that AB=BQ

Given: ABCD is a parallelogram with P as mid point of BC

To Show: AB=BQ

Steps	Statement	Reason
1	BP = PC	Given that P is mid point of BC
2	BPQ=CPD	Vertically opposite angles
3	PBQ=PCD	Alternate angles as AB\|\|DC
4	BPQ CDP	ASA Postulate
5	BQ = DC	Corresponding sides are equal
6	DC = AB	Opposite sides of parallelogram are equal
7	BQ = AB	From 5 and 6

6.8.7 Problem 2: In the adjoining figure, the bisectors of angles of a parallelogram ABCD enclose PQRS. Prove that PQRS is a rectangle.

Given: ABCD is a parallelogram. AP, BP, CR and DR are the angular bisectors of angles A, B, C and D respectively.

To Show: PQRS is a rectangle.

Steps	Statement	Reason
1	DAB+ADC= 180⁰	Sum of consecutive angles of a parallelogram =180⁰
2	DAB=2DAS	AP is bisector of DAB
3	ADC=2ADS	DR is bisector of ADC
4	DAS+ADS = 90⁰	Substituting values of angles in Step 1, from 2 and 3
5	DAS+ADS+ ASD= 180⁰	Sum of all angles in a triangle (ADS ) is 180⁰
6	ASD= 180⁰-(DAS+ADS)	Transposition
7	= 180⁰-90⁰= 90⁰	Substitute value from step 4
8	PSR =ASD	Vertically opposite angles are equal
9	= 90⁰
10	DAB +ABC =180⁰	Consecutive angles in a parallelogram
11	1/2DAB +1/2ABC =90⁰
12	PAB +ABP =90⁰	AP bisects A and BP bisects B
13	SPQ =90⁰	Sum of all angles in APB = 180⁰

Similarly we can show that PQR=QRS=90⁰

Hence PQRS is a rectangle.

6.8.7 Problem 3: PQRS is a parallelogram. PS is extended (produced) to M so that SM = SR and MR is extended to meet PQ extended at N.

Prove that QN=QR.

Given: PQRS is a parallelogram. SM=SR

To Show: QN=QR

Steps	Statement	Reason
1	SRM =SMR	SM=SR and hence SRM is an isosceles triangle
2	MSR =SPQ	Corresponding angles(SR\|\|PQ)
3	SPQ=RQN	Corresponding angles(PS\|\|QR)
4	MSR=RQN	Equating Step
5	SRM =QNR	Corresponding angles(SR\|\|PN)
6	SMR=QRN	Since two angles in MSR and NQR are equal, third angle also has to be equal (sum of 3 angles in a triangle = 180⁰)
7	QNR=SRM=SMR =QRN	From Step4, Step1, Step5
8	QN=QR	From Step 6, we conclude that QNR is an isosceles triangle

6.8.7 Problem 4: ABCD is a parallelogram. The bisectors of A and B meet BC and AD at X and Y respectively. Prove that XY=CD.

Given: ABCD is a parallelogram. AX bisectsA and BY bisectsB. Let AX and BY meet at O

To Show: XY=CD

Consider ABX and AXY

Data : AD ||BC and hence AY||BX, AB=CD,

Steps	Statement	Reason
1	BAX = AXY	Alternate angles AY\|\|BX and AX is transverse
2	XAY = AXB	Alternate angles AY\|\|BX and AX is transverse
	Consider BAY and XYB
3	BAY = YXB	Sum of angles in step 1 and step 2
4	BY is common side
5	AYB = YBX	Alternate angles AY\|\|BX and BY is transverse
6	BAY XYB	ASA Postulate
7	AB =XY, AY=BX	Corresponding sides, Step 6
8	XY =CD	AB=CD(given), step 7

6.8.7 Problem 5: ABCD is a parallelogram with AB||CD. P is the mid point of AB and CP bisects BCD. Prove that CPD =90⁰

Hint: If we can prove that PDC+ PCD =90⁰ then it follows that CPD =90⁰

1. Note that PBC is an isosceles triangle (DCP = CPB = PCB as AB||CD and CP is a transverse)

2. Prove that ADP is an isosceles triangle (AD=BC, AP=PB and PB=BC and hence AD=AP)

3. DP bisects ADC (AB||CD and DP is a transverse)

4. ADC + DCB = 180⁰ (Sum of 2 consecutive angles of a parallelogram)

5. 2(PDC+ PCD) = 180⁰(follows from step 4)

6. CPD =90⁰(sum of all angles in a triangle = 180⁰)

6.8.7 Theorem 3: Parallelograms standing on the same base and between same parallel lines have equal areas.

Data: ABCD and ABEF are two parallelograms standing on the same base AB and between same parallel lines PQ and RS

To prove: Area of ABCD = Area of ABEF.

Proof:

Steps	Statement	Reason
	Consider FAD and EBC
1	AF = BE	Opposite sides of ABEF.
2	AFD = BEC, ADF = BCE,	Corresponding angles of AF\|\|BE and AD\|\|BC, PQ is transversal
3	FAD = EBC	When two angles of triangles are equal, third angle also has to be equal
4	FAD EBC	ASA Postulate
5	Area of FAD = Area of EBC	Congruent triangles have equal area.
6	Area of FAD+ Area of DEBA = Area of EBC+ Area DEBA	Adding area of quadrilateral DEBA to both sides.
7	i.e. Area of FEBA = Area of ABCD	If equals are added to equals, then the resulting sums are also equal.

This proves the theorem.

Note: Earlier we have seen that the area of parallelogram is product of base and its altitude (height). Since PQ and RS are parallel lines, the altitudes

of FEBA and ABCD are equal. Since the parallelograms, FEBA and ABCD have the same base AB, it follows that the parallelograms have same area.

6.8.7 Corollary 1: Parallelograms standing on equal base and between same parallel lines have equal areas.

Note: We know that the area of parallelogram

is product of base and its altitude (height)(Refer 6.8.2)

Since PQ and RS are parallel lines,

the altitudes of EFGH and ABCD are equal.

Since the parallelograms, EFGH and ABCD have equal bases

(AB=EF),

it follows that the parallelograms have same area.

6.8.7 Corollary 2: If a parallelogram and a triangle stand on the same base and between same parallel lines, then the area of triangle is half the

area of the parallelogram.

Note:

We know that the area of parallelogram (ABCD) is

product of its base and its altitude (height) (=AB*h).*(Refer 6.8.2)

We have also proved that diagonal divides a parallelogram in to two

congruent triangles (refer 6.8.7 Theorem 2)

ADB CDB

Area of parallelogram ABCD = area of ADB + area of CDB

= 2 *area of ADB

Area of ADB = half the area of parallelogram.

=1/2( AB*h) = 1/2 base *height

Note : So far we have been using the formula for area of a triangle = 1/2 base *height, without proof.

In the process of proving above corollary, we have also arrived at the formula for calculation for the area of triangle.

6.8.7 Corollary 3: Triangles standing on the same base and between same parallel lines are equal in area.

We know that the area of a triangle is half the product of its base and its altitude

Area ofABC

= (1/2)*base*height = (1/2)*AB*h

In addition, we know that the distance (h) between any two parallel lines is always fixed.

Hence ABD has the same height ‘h’ as ABC.

Area of ABD = 1/2(AB*h)

Area of ABC= Area of ABD

Note: We can also prove the above by constructing two parallelograms one || AC and another ||BD with AB as common base and using theorem 6.8.7

Theorem 3 and 6.8.7 Corollary 2.

6.8.7 Corollary 4: Triangles standing on equal base and between same parallel lines are equal in area.

(By formula, area of triangle is half of its base and height).

6.8.7 Problem 6: In the given figure DE||BC, prove that the area of BOD = Area of COE

Given: DE ||BC

To Show: Area of BOD= Area of COE

Steps	Statement	Reason
1	Area of BCD= Area of BCE	BC is the common base for both BCD and BCE. Both triangles have same height as DE\|\|BC.
2	Area ofBCD- Area of BOC =Area of BCE -Area of BOC	The common area of triangle BOC is subtracted from the areas of both the triangles of Step 1
3	Area of BOD= Area ofCOE

6.8.7 Problem 7: In the given figure, D and E are the points on the sides AB and AC respectively, such that the area ofBCE = Area ofBCD.

Show that DE||BC

Given: Area of BCE = Area of BCD

To Show: DE || BC

Steps	Statement	Reason
1	Area ofBCE = 1/2 BC*altitude of BCE	Formula for area of the triangle with BC as base
2	Area ofBCD = 1/2 BC*altitude ofBCD	Formula for area of the triangle with BC as base (BC is common base)
3	BCaltitude ofBCE= BCaltitude ofBCD	It is given that areas of both the triangles are same
4	Altitude ofBCE = Altitude of BCD	From step 3
5	DE \|\| BC	Distance between two lines are same

6.8.7 Mid-Point Theorem: The line joining the mid points of any two sides of a triangle is parallel to third side and is equal to half the third side.

Data: In triangle ABC, D and E are mid points of AB and AC respectively

To prove: DE||BC and DE=1/2BC.

Construction: From C, draw a line parallel to AB. Extend DE to meet this line at F

Proof :

Steps	Statement	Reason
	Consider ADE and ECF
1	AE = CE	E is midpoint of AC
2	BAE = ECF	Alternate angles of AB\|\|CF
3	ADE = CEF	Vertically opposite angles
4	EDA EFC	ASA Postulate
5	DE=EF,AD=CF	Corresponding sides are equal
6	AD=DB	Given that D is midpoint of BA
7	DB=CF	From step 5 and step 6
8	DBCF is a parallelogram	Opposite sides CF and BD are equal and parallel
9	DF\|\|BC,DF=BC	From Step 8
10	DE=EF	From Step 5
11	BC = 2DE	From Step 9 and Step 10

6.8.7 Converse of midpoint theorem: The straight line drawn through the mid point on one side of a triangle and parallel to another

bisects the third side.

Data: In triangle ABC, D is mid point of AB. DE||BC

To prove: E is mid point of AC

Construction: From C draw a line parallel to AB. Extend DE to meet this line at F

Proof:

Steps	Statement	Reason
1	BD = CF	DBCF is parallelogram
2	AD = BD	Given D is mid point of AB
	Consider ADE and ECF
3	AD=CF
4	BAE = ECF	Alternate angles of AB\|\|CF
5	AED = CEF	Vertically opposite angles
6	ADE ECF	ASA Postulate
7	AE=EC	Step 6

6.8.7 Problem 8: Prove that the figure obtained by joining the mid points of adjacent sides of a quadrilateral is a parallelogram.

Given: P, Q, R, S are the mid points of AB, BC, CD, DA respectively, of quadrilateral ABCD.

To Show: PQRS is a parallelogram

Construction: Join BD.

Steps	Statement	Reason
1	PS\|\|BD and 2PS=BD	Midpoint theorem forABD with P and S as mid points of AB and AD respectively
2	BD\|\|RQ and 2RQ=BD	Midpoint theorem forCDB with Q and R as mid points of BC and CD
3	i.e. PS\|\|RQ and 2PS=2RQ or PS=RQ	From Step 2
4	PSRQ is a parallelogram	From Step 3

6.8.7 Problem 9: Prove that the figure obtained by joining mid points of the adjacent sides of a rhombus is a rectangle

Given: P, Q, R, S are the mid points of AB, BC, CD, DA respectively of quadrilateral ABCD

To Show: PQRS is a rectangle.

Construction: Join BD and AC

Proof:

Firstly, follow the steps described above to show that PQRS is a parallelogram.

Steps	Statement	Reason
1	AO=OC,OD=BO and AOD= 90⁰	In a rhombus diagonals bisect each other perpendicularly
2	DAO+ADO+AOD =180⁰	Sum of angles in a triangle
3	DAO+ADO =90⁰	Step 1, Step 2
4	DAO =DSR	SR\|\|AC and DAO,DSR are corresponding angles
5	PS\|\|BD	(Mid point theorem)
6	ADO =ASP	Corresponding angles(Step 5)
7	DSR+ASP =90⁰	Step3,Step 4 and Step 6
8	PSR = 180⁰-DSR+ASP = 180⁰-90⁰=90⁰	ASD is a straight line and step 7
9	SRQ = RQP =QPS =90⁰	Similar steps 2 to Step 8

6.8.7 Problem 10: In the following figure with AB||CD, prove that R is the mid point of BC and PR = 1/2(AB+DC)

Given: P and Q are midpoints of AD and BD respectively, AB||CD

To Show: R is mid point of BC, PR = 1/2(AB+DC)

Steps	Statement	Reason
1	PQ\|\|AB and PQ=1/2AB	Midpoint theorem for ABD with P and Q as mid points of AD and BD
2	R is mid point of BC	Converse of midpoint theorem for DBC with Q as mid point of DB and PR\|\|DC
3	QR=1/2CD	Midpoint theorem for DBC with R and Q as mid points of BC and BD respectively
4	PR =PQ+QR = 1/2AB+1/2CD	From Step 1 and Step 3
5	i.e. PR = 1/2(AB+DC)

Note: From this we conclude that the length of the line segment joining mid points of two non parallel sides of a trapezium is half the sum

of lengths of the parallel sides.

6.8.7 Problem 11: D, E and F are midpoints of AB, AC and BC of an isosceles triangle ABC in which AB=BC. Prove that DEF is also isosceles.

Given: D, E and F are midpoints of AB, AC and BC respectively, AB=BC

To Show: DEF is an isosceles triangle (any two sides in DEF are equal).

Solution:

Steps	Statement	Reason
1	2DE = BC	Midpoint theorem forABC with D and E as mid points of AB and AC
2	2FE = AB	Midpoint theorem forABC with E and F as mid points of AC and BC
3	AB=BC	Given
4	2DE=2FE, DE=FE	Substituting results of step 1 and step 2 in step 3

6.8 Summary of learning

No	Points to remember
1	The diagonals of a parallelogram bisect each other
2	Each diagonal divides the parallelogram in to two congruent triangles
3	Parallelograms standing on the same base and between the same parallel lines have equal areas
4	The line joining the mid points of any two sides of a triangle is parallel to and half the third side

Some useful formulae for calculation of areas:

Type	Figure	Area
Triangle		1/2 ah 1/2 base*height OR Where s = (1/2) (a+b+c) =1/2(sum of sides)
Quadrilateral		(1/2) d(h1+h2) 1/2 diagonal * sum of altitudes on the diagonal
Parallelogram		ah (baseheight)
Trapezium		(1/2) h(a+b) (1/2) product of height and sum of parallel sides
Rectangle		ab Product of sides
Square		a*a = a² Square of sides
Rhombus		(1/2)ab (1/2) product of diagonals

Additional Points:

6.8.7 Intercept Theorem: If three or more lines make equal intercepts on one transversal, then they make equal intercepts on any other transversal.

Given: Transversal p makes equal intercepts (AB=BC) on three lines l, m and n.

(i.e. l || m || n) q is another transversal which makes intercepts DE and EF.

To prove: DE=EF.

Construction: Draw AS and BT parallel to the line q.

Steps	Statement	Reason
	Consider ABS and BCT
1	ABS = BCT, BAS = CBT,	Corresponding angles (It is given that line l \|\| line m)
2	AB=BC	Given
3	ABS \|\|\| BCT	ASA postulate on congruence.
4	AS=BT	Corresponding sides are equal

5	ASED is a parallelogram	AS\|\|DE(construction), AD\|\|BE(Given)
6	AS=DE	Sides of a parallelogram
7	BTFE is a parallelogram	BT\|\|EF(construction), BE\|\|CF(Given)
8	BT=EF	Sides of a parallelogram
9	DE=EF	Steps 4,6 and 8

6.8.7 Problem 12: D, E and F are the mid points of the sides AB, BC and CA of the triangle ABC. AE meets DF at O. P and Q are mid points of

OB and OC respectively. Prove that DPQF is a parallelogram.

Steps	Statement	Reason
	Consider ABC
1	DF\|\|BC and 2DF = BC	Mid point theorem (D and F are mid points)
	Consider BOC
2	PQ\|\|BC and 2PQ = BC	Mid point theorem (P and Q are mid points)
	Consider ABO
3	DP\|\|AO and 2DP = AO	Mid point theorem (D and P are mid points)
	Consider ACO
4	FQ\|\|AO and 2FQ = AO	Mid point theorem (F and Q are mid points)
5	DF = PQ, DF\|\|PQ	Steps 1,2
6	DP = FQ, DP\|\|FQ	Steps 3,4

6.8.7 Problem 13: In a trapezium ABCD, AB||DC, P and Q are mid points of AD and BC respectively. BP produced meets CD produced at point E.

Prove that P bisects BE and PQ||AB.

Steps	Statement	Reason
	Consider BAP and EDP
1	EPD = BPA	Vertically opposite angles
2	PD = PA	Given (P is mid point of AB)
3	ABP = PED	Alternate angle AB\|\|DE
4	BAP EDP	ASA Postulate
5	PE=PB	Step 4
	Consider EBC
6	P and Q are mid points of sides EB and BC respectively	Step 5 and given
7	PQ\|\|DC	Mid point theorem
8	DC\|\|AB	Given
9	PQ\|\|AB	Step 7 and 8

6.8.7 Theorem 4: In a parallelogram prove that opposite sides and opposite angles are equal

Data: In ABCD AB||CD and AD||BC

To Prove: AD=BC, AB=CD and ADC = ABC and DAB = DCB

Construction: Join BD

Steps	Statement	Reason
	Consider ADB and BCD
1	CDB = DBA	Alternate angle AB\|\|CD
2	BD is common	Construction
3	ADB = DBC	Alternate angle AD\|\|BC
4	ADB BCD	ASA Postulate
5	AD=BC, AB=CD	Step 4
6	DAB = BCD	Step 4
7	CDB + ADB= DBA+DBC	Addition of Step 1 and 3
8	ADC = ABC	Simplification of step 7

Exercise: Prove the following:

No	Theorems:
1	A quadrilateral is a parallelogram if their diagonals bisect each other
2	A quadrilateral is a parallelogram if their opposite sides are equal
3	A quadrilateral is a parallelogram if their opposite angles are equal
4	A quadrilateral is a parallelogram if a pair of opposite sides is equal and parallel
5	A parallelogram is a rectangle if their diagonals are equal
6	A parallelogram is a square if their diagonals are equal and intersect at right angles
7	A diagonal of a square makes an angle of 45^o with the sides of the square
8	A parallelogram is a rhombus if adjacent sides are equal
9	A diagonal of a rhombus bisects vertex angles
10	The diagonals of a rhombus intersect each other at right angles
11	A parallelogram is a rhombus if their diagonals intersect at right angles
12	A rhombus is a square if their diagonals are equal

Hint: Use the following properties/statements to prove all of the above theorems after drawing diagonals if required.

1. SSS/ASA/SAS postulates for congruency of triangles.

2. Alternate/Corresponding angles are equal when lines are parallel.

3. In an isosceles triangle angles opposite to equal sides are equal.

6.8.7 Problem 14: ABCD is a parallelogram. A line through A cuts DC at point P and BC produced to Q. Prove that area of BCP = area of DPQ

Construction: Draw AEBC and CFAB

Steps	Statement	Reason
1	Area of ABCD = ABCF=ADAE=BC*AE	Formula for area and AD=BC
2	Area of ADQ = (1/2)ADAE	Formula for the area of
3	Area of ABP = (1/2)ABCF	Formula for the area of
4	Area of ADQ = Area of ABP	ADAE=ABCF(step 1),Step2,3
5	Area of ADQ = Area of ADP + Area of DPQ	From figure
6	Area of ADP + Area of BCP= Area of ABCD - Area of ABP= ABCF – (1/2)ABCF = (1/2)ABCF	From figure Step 1,3
7	= Area of ABP	Step 3
8	Area of ADP + Area of BCP = Area of ADP + Area of DPQ	Step 4 and 5
9	Area of BCP = Area of DPQ	Simplification of step 8

Their Name:
Their Email:
Your Email:
Your Name:
Your message to your friend: