3.2 Sets- Part 1:

3.2 Example 1:

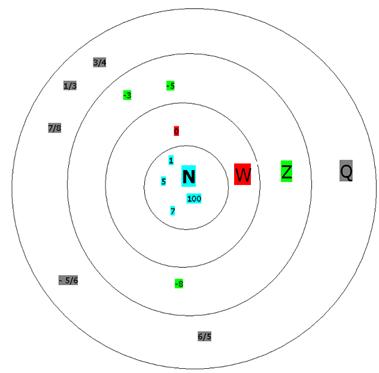
In topic 1.1 we have studied different type of numbers and let us try to represent them using set notations.

N = {Set of natural numbers},

W={Set of whole Numbers},

Z= {Set of integers} and

Q= {set of rational numbers}

Then N W Z Q

Note All these are infinite sets.

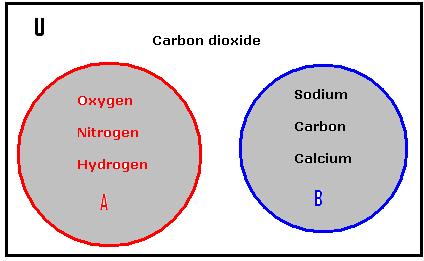
3.2 Example 2: Let us consider the sets U = {Oxygen, Nitrogen, Hydrogen, Carbon dioxide, Sodium, Carbon, Calcium} A = {Oxygen, Nitrogen, Hydrogen}

B = {Sodium, Carbon, Calcium}

Note that both A and B are subsets of U.

Definition :

1) The ‘union’ (represented by the symbol ) of two sets is defined as a set of all those elements which are either in A or in B or in both A and B. AB is pronounced as A union B.

Thus in this example AB = {Oxygen, Nitrogen, Hydrogen, Sodium, Carbon, Calcium}.

In the adjoining figure, the portion represented by grey colors is AB.

2. The ‘intersection ’(represented by the symbol ) of two sets is defined as a set of all those elements which are present both in A and B.. The Symbol is pronounced as intersection. AB is pronounced as A intersection B

In this example, note that sets A and B do not have any common element. When two sets do not have common elements then they are called ‘disjoint’ sets.

Note that in this example A and B are disjoint sets as they do not have any common element. Therefore AB ={ }=(Null set)

The representation of sets U, A and B as shown in the figure (in circular shape or oval shape) is called representation by Venn diagram.

In Venn diagram, the universal set is represented by a rectangle and sub sets are represented by circles or ovals.

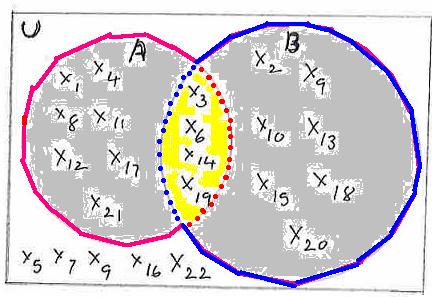
3.2 Example 3 : Let your class have a strength of 22. Assume that out of these, 11 are members of the cricket team. Also assume that you have a Hockey team of 11 players from these 22 students.It is possible that few may be members of both the team and few may not be members of any team.

The Venn diagram drawn on the right helps us to find the players who are members of both the teams and students who are not members of any team.

Let U represent the set of students in your class.

U = { X₁,X₂,X₃…………X₂₂)

Let A be the players representing cricket team.

A = { X₁,X₃, X₄,X_6, X₈,X₁₁,X₁₂, X₁₄,X₁₇,X₁₉,X₂₁)

Let B be the players representing hockey team.

B = { X₂,X₃,X₆.X₉,X₁₀,X₁₃,X₁₄,X₁₅,X₁₈,X₁₉,X₂₀}

How do we find players who represent both teams?

How do you find players who are not in any team?

We find that { X₃,X₆,X₁₄,X₁₉} is the set of four players who are in both the teams.

The set AB ={ X₁,X₂, X₃,X_4, X₆,X₈, X₁₀,X₁₁,X₁₂,X₁₃,X₁₄,X₁₅,X₁₇,X₁₈, X₁₉,X_20, X₂₁) is the set of players who are in Cricket team or Hockey team.

This is the grey+ yellow+grey colored portion of the figure.

We can represent these sets using Venn diagrams as given on the right hand side.

The section shaded in yellow color is the set of students who are in both the teams and is represented by AB.

We also find that {X₅,X₇,X₉,X₁₆,X₂₂} is the set of five students who are not in any team.

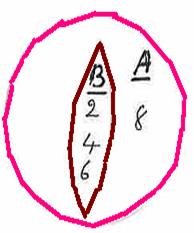
3.2 Example 4 : Let A = { 2,4,6,8}, Let B = { 2,4,6} = { }

Observations:

Since in a set, the elements are written only once

AA = {2,4,6,8} = A

Since is a subset of every set ,

A ={ 2,4,6,8} = A

If B A then BA = {2, 4,6,8}= A

IF B A then AB = {2,4,6} = B

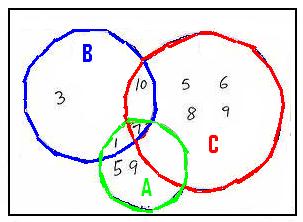
3.2 Problem 1: Draw the Venn diagram for ABC and ABC if A = {1,5,7,9} and B={1,3,7,10} and C= {5,6,7,8,9,10}

Solution :

Set A is represented by the green colored circle.

Set B is represented by the blue colored circle.

Set C is represented by the red colored circle.

(AB)C = ({1,3,5,7,9,10}){5,6,7,8,9,10} = {1,3,5,6,7,8,910}

(AB)C = ( { 1,7}{5,6,7,8,9,10} = {7}

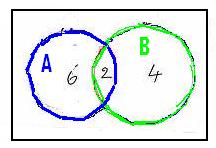
3.2 Problem 2: A = {x: x²-8x+12 =0} and B = {x: x²-6x+8 =0} Find AB and AB

Solution :

We know that x²-8x+12 = (x-6)(x-2). Thus x²-8x+12 = 0 is true when x=6 or x=2

We know that x²-6x+8 = (x-4)(x-2). Thus x²-6x+8 = 0 is true when x=4 or x=2

Therefore A = {6,2) (represented by blue colored circle)

and B= {4,2} (represented by green colored circle).

Hence AB = {6, 4, 2}, AB ={2}

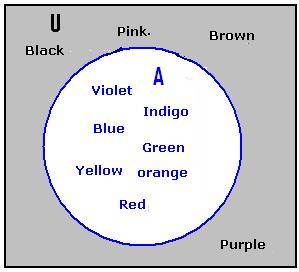
Let U = (Black, Pink, Brown, Purple, Violet, Indigo, Blue, Green, Yellow, Orange, Red}

A = {Violet, Indigo, Blue, Green, Yellow, Orange, Red}

The sets can be represented by a Venn diagram as shown in the adjoining figure.

Let us consider the set {Black, Pink, Brown, Purple}

What is special about this set? This set has elements of U which are not in A.

It is called ‘complement' of set A and is denoted by A¹_.

So A¹={Black, Pink, Brown, Purple}

Definition : A set is said to be ‘complement’ to another set U, if the elements in that set has elements which are in U but not in itself . The complement of set A is denoted by A¹_.

We notice that A¹ U and A A¹=U and AA¹=( The sets A and A¹ do not have any common element).

(A¹)¹ = {elements of U which are not in A¹}

= {Violet, Indigo, Blue, Green, Yellow, Orange, Red}= A

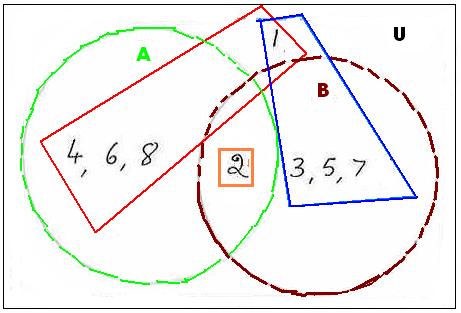
3.2 Problem 3: If U = {Natural numbers less than 9}, A = {Even numbers less than 9}, B = {Prime numbers less than 9}

Find A¹B¹ and A¹B¹

Solution :

We have

U = {1,2,3,4,5,6,7,8}, A = {2,4,6,8}, B = {2,3,5,7}

A¹= { 1,3,5,7}( covered by blue colored quadrilateral ),

B¹= { 1,4,6,8}( covered by red colored quadrilateral)

A¹B¹ = {1,3,4,5,6,7,8}

A¹B¹= {1}

Let us find (AB)¹ and (AB)¹

AB= {2,3,4,5,6,7,8}

(AB)¹= {1}

AB = {2}( covered by orange colored square)

(AB)¹= { 1,3,4,5,6,7,8}

What do we notice?

(AB)¹= A¹B¹ and (AB)¹= A¹B¹

If A and B are two sets then the ‘difference’ set (A-B) is defined as a set which has elements of A but not of B.

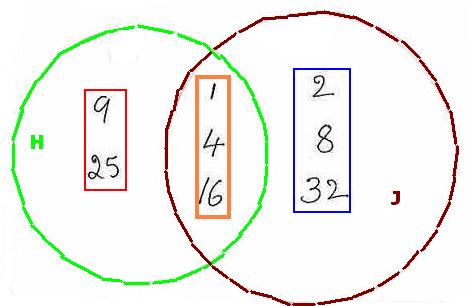
3.2 Example 5 : Let H = {Squares of natural numbers less than 36} J = {1, and multiples of 2 less than 34} Find HJ H-J and J-H

We have

H = { 1,4,9,16,25}, J = {1,2,4,8,16,32}

HJ = {1,4,16}( covered by orange colored rectangle)

H- J = {elements of H not in J}

= {9,25}(covered by red colored rectangle)

J - H = {elements of J not in H}

= {2,8,32}(covered by blue colored rectangle)

Notice that H-J J-H

Observations:

For any sets U and A

()¹=U and(U)¹=

A-A=

3.2 Summary of learning

No	Points to remember
1	Definitions of sets(Union, Intersection, compliment, difference)
2	Venn diagram

Their Name:
Their Email:
Your Email:
Your Name:
Your message to your friend: