5.5 Standard Deviation:

Introduction:  

You must have read newspapers comparing performances of two batsmen in cricket. What do they compare? They say one is more consistent than the other and one is more stylish than the other.

Stylishness is a quality which cannot be compared using runs scored by batsmen. However, they compare one being better than the other and their consistency in batting, based on the runs scored in several innings.

Let us study how Statistics can help us in this regard.

 

Standard deviation:

You must have heard people talking about deviations (deviation in rules, deviation in works, deviation in results, etc)? Deviation is always compared with respect to a standard.

 

Standard could be thought of as an average (also called arithmetic mean).


5.5 Example 1:  Let a batsman’s score in 6 innings be 48,50,54,46,48,54

 

Working:

Notations used:

X = Set of scores (48,50,54,46,48,54)

N = Number of scores (=6)

 =The Arithmetic mean (AM) = ()/N

d = Deviation from the arithmetic mean = X -

Step 1: Find the Arithmetic mean of his scores (AM) = 50 =(48+50+54+46+48+54)/6

Step 2: Find d (= X-AM) and d2 for each of the scores

 

Table of Calculation: (with actual AM)

 

No

Runs(X)

Deviation (d)

= X-

(Deviation)2

  = d2

1

48

-2

 4

2

50

0

 0

3

54

 4

16

4

46

-4

16

5

48

-2

 4

6

54

 4

16

 

=300

=0

 = 56

Step 3: Calculate Variance as =/ N

Step 4: Calculate Standard deviation (SD) as =  =

SD is denoted by Greek letter.

In the above Example SD = = = = = 3.05.

Definition: ‘Standard deviation’ is the square root of the arithmetic average of the squares of the deviations from the mean.

Interpretation: In this example we say that on an average, the batsman’s scores deviate from the arithmetic mean (=50) by 3.05(3 ).

 

It can be predicted that, more or less this batsman is likely to score 47-53 {(50-3)-(50+3)} runs in future matches.

 

Note: If the batsman’s score were to be 48,100,50,10,2,80, it would not have been possible to predict reasonably accurately  . Since the batsman was consistent with scores around 50, it was possible to predict.

 

General Procedure:

 

Let X = {x1, x2 , x3……….. xn} be the scores

N = Number of scores

* = Arithmetic mean (AM) = (x1+x2 + x3+…… xn)/N= / N

Step 1: Calculate deviation from AM, d (=X-) and d2 for each of the scores

 

Step 2: Calculate Variance = ()/ N

Step 3: Calculate Standard deviation (SD)

 SD = =

 

Alternate method of finding, when AM is not a whole number.

 

In the above example the Arithmetic mean (=50) happened to be an integer and our computations became easy. If arithmetic mean contains decimals, finding d2 will be tough and in such cases we follow a different method.  To start with, we assume Arithmetic mean to be one of the scores itself. Then we calculate d (= X-A where A is the assumed AM) and d2 for each of the scores. Then actual AM and SD are derived as follows:

 

Actual AM = Assumed AM + ()/N

SD () =  [(d2)/N - ((d)/N)2]

Let us take the above example and find SD using this alternate method.

Let us assume AM to be 54 (A = 54.) Here N = 6.

Table of Calculation (with assumed AM)

 

No

Runs(X)

Deviation(D)

 d= X-A

(Deviation)2

  = d2

1

48

-6

36

2

50

-4

16

3

54

0

0

4

46

-8

64

5

48

-6

36

6

54

0

0

 

 

= -24

= 152

 

Actual AM = Assumed AM + ()/N= 54 + (-24/6) = 54-4 = 50

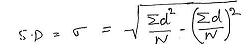
SD() =  [(d2)/N - ((d)/N)2]

 =   [152/6 –(24/6)2] =  (25.33-16) =  (9.33) =3.05

 

You will notice that both the methods give same SD in all cases.

When same scores repeat many times in the data, we follow a slightly different method as listing individual scores and calculating SD becomes tedious.

 

Standard Deviation for grouped data:

 

Let the scores and frequencies be

 

Scores(X)    -------ŕ

X1

X2

X3

……

Xn

Frequency(f) ------ŕ

f1

f2

f3

……..

fn

N = Total number of frequencies = f1 + f2 + f3 +…….. fn=

Step 1: Find f*x for each of the scores

Step 2: Find the Arithmetic mean = ()/N

Step 3: Find deviation for each of the score d = (X-)

 

Step 4: Find the variance of distribution = ((f*d2))/N

Step 5: Calculate SD() =  [((f*d2))/N]

5.5 Example 2: Marks obtained in a test by 60 students are given below. Find AM and SD.

 

Scores(X)    -------ŕ

10

20

30

40

50

60

Frequency(f) ------ŕ

8

12

20

10

7

3

 

Workings:

N (Total number of frequencies) = = 8+12+20+10+7+3=60

 

Score(X)

Frequency(f)

fX

Deviation=

(X-)

d2

f*d2

10

8

80

-20.83

433.89

3471.11

20

12

240

-10.83

117.29

1407.47

30

20

600

-.83

0.69

13.78

40

10

400

9.17

84.09

840.89

50

7

350

19.17

367.49

2572.42

60

3

180

29.17

850.89

2552.67

 

N==60

= 1850

 

 

(f*d2)=10858.33

Arithmetic Mean == ()/N= 1850/60 =30.83

Variance = (f*d2)/N = 10858.33/60= 180.97

SD () =  [(f*d2)/N] = (180.97) =13.45

Interpretation: An average mark of students is 30.83. The marks of students deviate from the Mean score by about 13 marks.

In the above working you must have observed that AM had decimals. Because of this reason d, d2 and f*d2 were all decimals and calculations were difficult.

In such cases we use an alternate method which is easier to work with.

 

Alternate Method

 

Step 1:  Assume any of the score as Average (A)

 

Step 2: Find the deviation d, from the assumed average for every score (d=X-A).

 

Step 3: Find f*d, d2 ,f*d2 for each of the scores.

 

Step 4: Arrive at AM and SD as given below.

Arithmetic Mean == A + /N, where N =

SD ()= [(f*d2)/N - ((f*d)/N)2 ]

 

In the above example let us assume 30 to be the  Average (A) and by following steps 1 to 3 we get

 

Score(X)

Frequency(f)

Deviation(d)

=X-A

f*d

d2

f*d2

10

8

-20

-160

400

3200

20

12

-10

-120

100

1200

30

20

0

0

   0

0

40

10

10

100

100

1000

50

7

20

140

400

2800

60

3

30

90

900

2700

 

N==60

 

=50

 

(f*d2)=10900

 

We note that AM = A+ ()/ (N) = 30+50/60 = 30+0.83= 30.83

 

SD () =  [(f*d2)/N - ((f*d)/N)2]

=  [(10900/60) – (50/60)2]

=  (181.67 - 0.69) = (180.97) =13.45

 

The average mark of students is 30.83. The marks of students deviate from the Mean score by about 13 marks.

Observe that we got same results in both the methods.

 

We have seen earlier that many times data is collected in class intervals and not as individual scores. In such cases we need to calculate AM in a different ways and not as average of scores.

How to find SD and interpret results if we have grouped data?

 

Step 1: Find the mid-points(x) for each of the class interval.

 

Step 2: Find the product f*x for each of the class interval.

Step3: Calculate the arithmetic mean == ( )/N, where N = .

 

Step 4: Find the Deviation d from the arithmetic mean () for each the class intervals. (d=X-)

 

Step 5: Find d2 and f*d2 for each of the class interval.

 

Step 6: Calculate SD using the formula SD () =  [(f*d2)/N]

 

5.5 Example 3: Marks obtained in a test by students are

 

Marks

Frequency(f)

Mid-point(x)

f*x

d=X-)

d2

f*d2

25-30

5

28

140

-9.2

84.64

423.2

30-35

10

33

330

-4.2

17.64

176.4

35-40

25

38

950

0.8

0.64

16

40-45

8

43

344

5.8

33.64

269.12

45-50

2

48

96

10.8

116.64

233.28

 

N = = 50

 

=1860

 

 

(f*d2)=1118

 

Working:

Arithmetic mean== /N = 1860/50 = 37.2

 

SD () =  [(f*d2)/N] =  (1118/50) =  (22.36) =4.728

 

Interpretation: The average marks scored is 37.2. The marks of students deviate from the Mean (average) score by about 5 marks.

 

In the above working you must have observed that AM had decimals. Because of this reason d, d2 and f*d2 had decimals and calculation was difficult. In such cases we use an alternate method which is easier to work with.

 

Alternate Method (Step – Deviation Method)

 

Step 1: Assume  one of the middle values of the class interval as the arithmetic mean (A).

 

Step 2: Find the ‘step-deviation’ (d) from the assumed mean d=(X-A)/i: Where ‘i’ is the size of the class interval

 

Step 3: Find d2, f*d and f*d2 for each of the class intervals

 

Step 4: Compute AM and SD  as follows

AM = Arithmetic mean== A + [/N]*i 

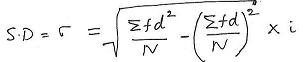
SD () =  [(f*d2)/N - ((f*d)/N)2]*i

 

Let us workout the above example using this method

In the above example let us assume mean (A) to be 43. Note i = size of class interval = 5.

By following steps 1 to 3 we have:

 

Marks

Frequency(f)

Mid-point(x)

d=(X-A)/i

f*d

d2

f*d2

25-30

5

28

-3

-15

9

45

30-35

10

33

-2

-20

4

40

35-40

25

38

-1

-25

1

25

40-45

8

43

0

0

0

0

45-50

2

48

1

2

1

2

 

N = = 50

 

 

= - 58

 

(f*d2)=112

 

We have

AM = Arithmetic mean== A+ [/N]*i = 43 + [(-58/50)*5] = 43 + (-1.16)*5 = 43-5.8 = 37.2

SD () =  [(f*d2)/N - ((f*d)/N)2]*i

=  [(112/50)- {-58/50} 2]*5

=  [2.24 - {-1.16} 2]*5

=  [2.24 – 1.3456]*5

=  [0.8944]*5

=.9457*5

=4.728

Interpretation: The average marks scored is 37.2. The marks of students deviate from the Mean (average) score by about 5 marks.

 

Very often we use the word consistency in comparing performances of individuals, teams, etc. How do we convert this adjective statistically?

 

We use the term ‘Co efficient of variation’ to measure the consistency. It is a relative measure of dispersion. It is calculated as

CV = SD*100/AM.

Thus CV is independent of units and is expressed as %. Lower the percentage more is the consistency (If SD is a small figure when compared AM obviously the variation is less)

In the above Example CV = (4.728*100)/37.2 =12.68

 

5.5 Example 4: The runs scored by 2 batsmen A and B in six innings are as follows.

 

Batsman A

48

50

54

46

48

54

Batsman B

46

44

43

46

45

46

 

Determine who is a better scorer ?. Who is more consistent?

 

Working:

 

To know the consistency of these two batsmen we need to find CV.

We have arrived at following values for AM and SD  for Batsman A in the Example (5.1) (worked out earlier)..

AM = 50

SD = 3.05

CV =SD*100/AM = 3.05*100/50 =6.1%

Let us calculate these figures for Batsman B

 

Table of Calculation: (with actual AM) AM = 270/6 = 45

 

No

Runs(X)

Deviation (D)

d= X-

(Deviation)2

  = d2

1

46

1

1

2

44

-1

1

3

43

-2

4

4

46

1

1

5

45

0

0

6

46

1

1

 

=270

=0

=8

 

 

SD =  =  =  (/N)=  (8/6) = (1.33) = 1.15

 

CV =SD*100/AM = 1.15*100/45 =2.55%

Conclusion:

1. Since A’s AM is more than that of B (50>45), we conclude that A is a better scorer.

2. Since B’s CV is less than A’s (1.15<6.1), we conclude that B is more consistent.

 

5.5 Example 5: Marks obtained in a test by X standard students of 2 sections A and B are given below:

 

Marks

No of students in Section A

No of students in Section B

25-30

5

5

30-35

10

12

35-40

25

20

40-45

8

8

45-50

2

5

 

 

Which section’s performance is better and which sections performance is more variable (not consistent)?

 

We need to find AM and CV to answer these questions.

We have arrived at following values of AM and SD for section A’s marks in example 5.3. (Worked out earlier).

 

AM =37.2 and SD =4.728

 

CV =SD*100/AM = 4.728*100/37.2 =12.7%

Now let us arrive at AM and SD for Section B using Step-Deviation Method (A is assumed).

Step 1: Let us chose assumed mean A =38 (we can assume A=28,33,43,48 also)

 

Step 2: Find the step-deviation (d) from the assumed mean d=(X-A)/i: Where ‘i’ is the size of class interval = 5.

 

Step 3: Find d2, f*d and f*d2 for each of the class intervals

 

Step 4: Compute AM and SD as follows

AM = Arithmetic mean== A+ [/N]*i 

 

SD () =  [Sum (fd2)/N- {Sum (fd)/N} 2]*i:

 

Marks

Frequency(f)

Mid-point(x)

d=(X-A)/i

fd

d2

fd2

25-30

5

28

-2

-10

4

20

30-35

12

33

-1

-12

1

12

35-40

20

38

0

0

0

0

40-45

8

43

1

8

1

8

45-50

5

48

2

10

4

20

 

N = = 50

 

 

= - 4

 

Sum(fD2)=60

 

We have

AM = Arithmetic mean== A+ [()/N]*i  = 38 +[(-4/50)*5] = 38+ -0.08*5 = 38-0.4 = 37.6

SD () =  [(f*d2)/N - ((f*d)/N)2]*i

       =  [(60/50)- {-4/50} 2]*5

       =  [1.2 - {-0.08} 2]*5

       =  [1.2 – 0.0064]*5

       =  [1.1936]*5

       =1.0925*5 =5.4625

CV = SD*100/AM = 5.4625*100/37.6 =14.52%

 

Conclusion:

 

1. Since Section B’s AM is more than that of section A (37.6>37.2), we conclude that B’s performance is a better than A.

2. Since B’s CV is more than A’s (14.52>12.7), we conclude that Section B’s performance is less consistent (more variable) than Section A’s.

 

5.5 Example 6: In 2 factories A and B, located in the same industrial area, the average weekly wages in Rupees and SD are

 

Factory

Average wage in Rs.

SD of wage in Rs.

A

34.5

6.21

B

28.5

4.56

 

Determine which Factory has greater variability.

 

Workings:

We need to find CV

CV of Factory A = SD*100/AM= 6.21*100/34.5=18%

CV of Factory B = SD*100/AM= 4.56*100/28.5=16%

Conclusion:  Since Factory A’s CV > Factory B’s (18>16), A has more variability in wages. (Note: Though Factory A pays more salary to its employees, it has large difference in wages between its employees)

 

5.5 Summary of learning

 

X = Set of scores

 =The Arithmetic mean (AM)

d = Deviation from the arithmetic mean

f = frequency of score

i = size of class interval

x= Mid-point of class intervalX

 

 

No

Cases

Options

N=

AM=

Deviation

(d)

 

SD()

 

1

Individual

 

Scores

 

Number of scores

* =()/N

X-

A=Any score

Number of scores

* = A+ ()/N

X-A

2

Scores

with

frequency

 

* =/N

X-

A=Any score

* = A + /N

X-A

3

Class interval

 

with frequency

 

* = /N

X-

A = Any mid point

* = A+ [/N]*i

d=(X-A)/i

 

Hint: For Standard Deviation always remember the common formula:

 

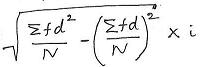
Depending on the options, you can substitute f=1 and i=1 to get the correct formula as per the above table.

Also note also that , =0 when any value is not chosen as an assumed average.

 

Additional Points:

 

Combined Standard deviation of two groups:

If the means and standard deviations of two series are known, then the mean and the standard deviation of the combined series can be calculated without considering the actual values of the data in the series.

 

Let the means and standard deviations of two series containing n1 and n2 values be X1 and X2 and SD1 and SD2 respectively. 

Then:

1.      The combined  mean = * = (n1 X1+ n2 X2)/( n1 + n2)

2.      The combined S.D. = {(n1 SD12 + n2 SD22 + n1 d12 + n2 d22)/( n1 + n2)} where d1 = X1-* and d2 = X2-*

 

5.5 Example 7: The first of the two samples has 100 items with mean 15 and standard deviation 3. If the combined group has 250 items with mean 15.6 and standard deviation. Find the mean and the standard deviation of the second group.

 

Solution:

Here n1 = 100, n1+n2 = 250, X1 = 15, SD =, *=15.6. We need to find X2 and SD2.

Note that n2=150. But

* = (n1 X1+ n2 X2)/( n1 + n2)

15.6 = (100*15+150* X2)/250

i.e. 150* X2= {(15.6*250) – (100*15)} = 3900-1500 = 2400

 X2 = 2400/150 = 16

d1= X1-* = 15-15.6 = -0.6, d2= X2-* = 16-15.6 = 0.4

S.D =  {(n1 SD12 + n2 SD22 + n1d12 + n2d22)/( n1 + n2)}

 = {(100*9 +150*SD22+100*0.36+150*0.16)/250}

13.44 = (900+150SD22+36+24)/250

i.e. 150SD22= 3360-960 = 2400

 SD22= 2400/150 = 16

 SD2 = 4

Thus the mean of the second group (X2) is 16 and the standard deviation of the second group (SD2) is 4.