2.16
ಚಕ್ರೀಯ
ಸಮಸಂಗತಿ (Cyclic Symmetry):
|
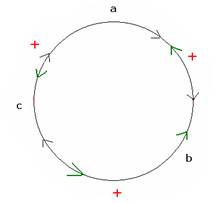
ಈ ಬೀಜೋಕ್ತಿಯನ್ನು ಗಮನಿಸಿ: a+b+c
--à(1) ಮೇಲಿನ ಬೀಜೋಕ್ತಿಯಲ್ಲಿ a ಯನ್ನು b ಯಿಂದ,, b ಯನ್ನು c ಯಿಂದ ಮತ್ತು c ಯನ್ನು a ಯಿಂದ - ಬದಲಾಯಿಸಿದಾಗ ನಮಗೆ ಹೊಸ ಬೀಜೋಕ್ತಿ ಸಿಗುತ್ತದೆಯೇ? b+c+a
-----à(2) ಪುನಃ b ಗೆ c, c ಗೆ a ಮತ್ತು a ಗೆ b, ಆದೇಶಿಸಿ. ಏನಾಗುತ್ತದೆ? c+a+b ---à(3) ಮೇಲಿನ ಮೂರೂ ಬೀಜೋಕ್ತಿಗಳು ಸರ್ವಸಮ. |
|
ಇಂತಹ ಸಂದರ್ಭದಲ್ಲಿ ನಾವು ಕೊಟ್ಟ
ಬೀಜೋಕ್ತಿ a+b+c
ಯನ್ನು a, b, c ಚರಾಕ್ಷರಗಳಲ್ಲಿ
‘ಚಕ್ರೀಯ’ (Cyclic) ಎನ್ನುತ್ತೇವೆ.
ಪುನಃ ಗಮನಿಸಿ: x2+y2+
z2 ಮತ್ತು x3+y3 +z3 ಇವುಗಳೂ x, y, z ಗಳಿಗೆ
ಸಂಬಂಧಿಸಿದಂತೆ ಚಕ್ರೀಯ..
ಬೀಜೋಕ್ತಿ a+b+c ಯನ್ನು ಹೀಗೆ
ಬರೆಯುತ್ತೇವೆ:
(‘ಸಿಗ್ಮಾ’ a)
ಅದೇ ರೀತಿ: x3+y3 +z3
= 
a-b+c ಬೀಜೋಕ್ತಿಯು ಚಕ್ರೀಯ ಸಮಸಂಗತಿಯೇ??
a,b,c ಗಳನ್ನು ಕ್ರಮವಾಗಿ ಬದಲಿಸಿದಾಗ ನಮಗೆ ದೊರೆಯುವ
ಬೀಜೋಕ್ತಿಗಳು b-c+a
ಮತ್ತು c-a+b
a=b=c ಆಗಿರದಿದ್ದರೆ ಇವು ಸರ್ವಸಮ ಆಗಲು ಸಾಧ್ಯವಿಲ್ಲ.
2.16 ಉದಾ 1: a2+b2+ c2-ab-bc-ca ಯನ್ನು 
ಉಪಯೋಗಿಸಿ ಬರೆ.
a2+b2+ c2-ab-bc-ca = (a2+b2+ c2)-(ab+bc+ca) =
( 
)or =(
)
2.16 ಉದಾ 2: ವಿಸ್ತರಿಸಿ 
= xy(x2-y2
)+yz(y2-z2)+zx(z2-x2)
2.16 ಕಲಿತ ಸಾರಾಂಶ
|
ಸಂ |
ಕಲಿತ ಮುಖ್ಯಾಂಶಗಳು |
|
1 |
ಚಕ್ರೀಯ ಸಮಸಂಗತಿಯನ್ನು ತಿಳಿಯುವುದು. |