6.12 Circles - Part 3:

 

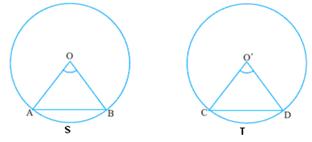
6.12.1: Arcs of a circle

 

Two arcs of two different circles having same radii are said to be ‘congruent’ if their central angles are same.

Arc ASB = Arc CTD if AOB = CO’D

 

6.12.1 Theorem 1: If two arcs are congruent then their chords are equal

Given: Arc ASB = Arc CTD

To prove: AB=CD

 

Proof:

1. OA = O’C, OB = O’D (Radii)

2. AOB = CO’D (it is given that arcs are congruent)

Hence by SAS Postulate on congruence AOB CO’D

Hence AB = CD

 

6.12.1 Theorem 2: If two chords of circles having same radii are same, then their arcs are congruent.

 

Note: This is converse of the previous theorem. (Use SSS postulate to show that AOB = CO’D)

 

6.12.1: Areas of sectors/segments of circle

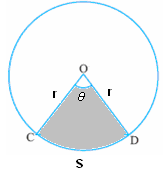
If ‘r’ is the radius of a circle, we know that :

Circumference of the circle = 2r,

Area of the circle = r2,                                 

Where  is a constant whose approximate value we use for our calculations is 22/7 (3.1428).

 

Let   (where  is in degrees) be the angle at center (COD) formed by the arc CSD.

Since  3600  at  the central angle  gives us  2r as the perimeter of the circle  then

 for  degree at the center, length of the arc made by it is

1. Length of the arc CSD = () *r (unitary method)

Since  3600  at  the central angle  gives us  r2 as the area of the circle  then

for   degree at the center, area of the sector made by  degrees:

 

2. Area of the sector CSDO (shaded portion in the adjoining figure) = () *r2

= () * ()= [() *r]*

= Length of the arc*()

Note:  radians = 1800 and x0 = () radians

 

 

 

 

 

 

 

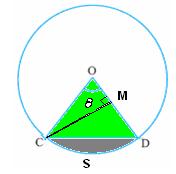
Let COD = in the adjoining figure with CD as chord

We note that

Area of triangle CDO = *base*height = *DO*CM = *r*rsin= r2*sin

(CM = rsin : Refer to section 7.1 for definition of sin of an angle)

 

From the figure we notice that

Area of Sector CSDO = Area of triangle CDO + Area of segment CSD  

Area of segment  CSD  = Area of Sector CSDO - Area of  CDO

= () *r2 - () r2*sin

= r2 {(*) - ()}

Note: For all the above calculations  must be in degrees.

 

 

      


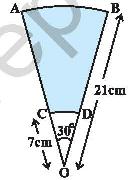
          6.12 Problem 1: AB and CD are respectively arcs of two concentric circles of radii 21Cm and 7Cm with center as O. IfAOB= 30,     find the area of the shaded portion

 

Area of the shaded portion CABD= area of OCABDO-area of OCDO

=  () *212  - () *72 ( 212=72 *32)

 

= **7*7*(3*3-1) ==

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

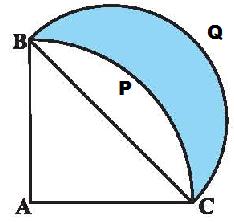
            6.12 Problem 2: In the figure, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region

 

 

Area of shaded region BPCQB= Area of semi circle BCQB- Area of sector  BCPB

But Area of sector BCPB = Area of quarter of circle ACPB- Area of  ABC

 Area of shaded region BPCQB =  Area of semi circle BCQB – ( Area of  quarter of circle  ACPB- Area of  ABC)

=  Area of semi circle BCQB – Area of quarter of circle ACPB + Area of  ABC

Note AC=AB=14  and BAC=90 

By Pythagoras theorem BC2 =  AB2 + AC2

BC(diameter) = =.  Radius  of semi circle BCQB=

Area of semi circle BCQB = *= **392= 154

Area of quarter of circle ACPB = 142 ( one fourth area of circle of radius 14cm)= **14*14=154

Area of  ABC = *14*14 = 98 ( Base and height of the triangle are same )

 Area of shaded region BPCQB= 154 -154 + 98 =98

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                                                                                                                                                                                          

 

 

 

 

 

 

 

 

 

6.12 Summary of learning

 

 

No

Points to remember

1

Congruency of arcs

2

Formula for length of an arc, Area of a segment