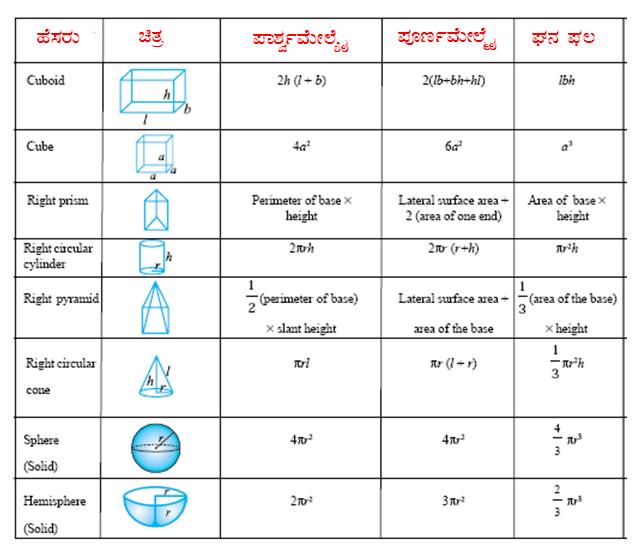
6.15 ಘನಾಕೃತಿಗಳು (Solid figures):

ನಮ್ಮ ದೈನಂದಿನ ವ್ಯವಹಾರದಲ್ಲಿ ನಮಗೆ ಎದುರಾಗುವ ಕೆಳಗೆ ಕಾಣಿಸಿರುವ ಸವಾಲುಗಳಿಗೆ ಉತ್ತರವಿದೆಯಾ ಎನ್ನುವುದನ್ನು ಇಲ್ಲಿ ಕಲಿಯುತ್ತೇವೆ

1. ಒಂದು ಹಾಲಿನ/ಪೆಟ್ರೋಲ್ ಟ್ಯಾಂಕ್ನಲ್ಲಿ ಎಷ್ಟು ಲೀಟರ್ ಹಾಲು/ಪೆಟ್ರೋಲ್ ಹಿಡಿಸುತ್ತದೆ?

2. ಬತ್ತದ/ರಾಗಿಯ/ಜೋಳದ/ಮರಳಿನ/ಜಲ್ಲಿ ಕಲ್ಲಿನ ರಾಶಿಯನ್ನು ನೆಲದ ಮಧ್ಯದಲ್ಲಿ, ಗೋಡೆಗೆ ತಾಗಿ, ಗೋಡೆಯ ಒಂದು ಮೂಲೆಯಲ್ಲಿ ಗುಡ್ಡೆ ಹಾಕಿದಾಗ ಅವುಗಳನ್ನು ಅಳೆಯುವುದು ಹೇಗೆ?

3. ಒಂದು ಕಂಭಕ್ಕೆ ಬಣ್ಣ ಹಾಕಲು ಎಷ್ಟು ಲೀಟರ್ ಬಣ್ಣ ಬೇಕು ಹಾಗೂ ಎಷ್ಟು ಕೂಲಿ ಕೊಡಬೇಕು.

4. ಒಂದು ಡೇರೆಯನ್ನು(ಟೆಂಟ್) ಕಟ್ಟಲು ಎಷ್ಟು ಬಟ್ಟೆ ಬೇಕು?

5. ಭೂಮಿಯ ಗಾತ್ರ, ಭಾರ ಎಷ್ಟು?

6.15.1 ಸಿಲಿಂಡರ್ (Cylinder)

ಸಿಲಿಂಡರಿನ ಹೊರಮೈ ವಿಸ್ತೀರ್ಣ:

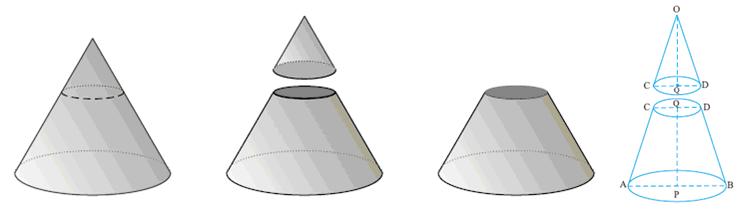
ನೀವು ನಿತ್ಯ ಜೀವನದಲ್ಲಿ ನೀರಿನ ಪೈಪುಗಳು, ರೋಡ್ ರೋಲರ್ನ ಚಕ್ರಗಳು, ಕಬ್ಬಿಣದ ಸರಳು, ಬಾವಿ, ಇವುಗಳನ್ನೆಲ್ಲಾ ನೋಡಿದ್ದೀರಿ. ಇವುಗಳೆಲ್ಲಾ ಸಿಲಿಂಡರ್ ಆಕಾರದಲ್ಲಿವೆ. ಅವುಗಳು ಪೈಪುಗಳ ರೀತಿ ಟೊಳ್ಳಾಗಿರಬಹುದು, ರೋಡ್ರೋಲರ್ ಚಕ್ರದಂತೆ ಘನವಸ್ತುವೂ ಆಗಿರಬಹುದು. ಅವೆಲ್ಲವುಗಳಿಗೂ ಎರಡು ಬದಿಗಳಲ್ಲಿ ವೃತ್ತಾಕಾರದ ಮೇಲ್ಮೈ (ಸಮತಲ) ಇರುತ್ತದೆ.

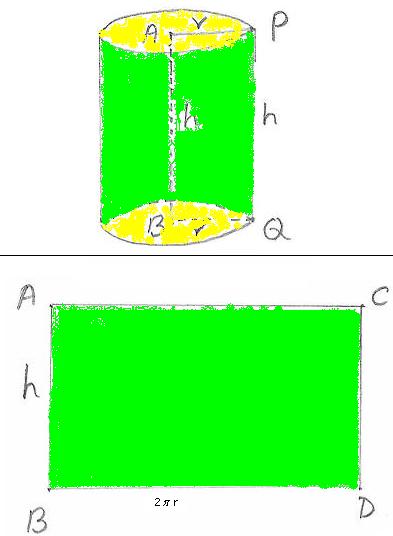
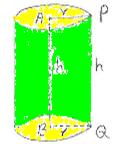
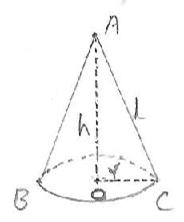
ಪಕ್ಕದ ಚಿತ್ರದಲ್ಲಿ AB ಯು ಸಿಲಿಂಡರಿನ ಅಕ್ಷ. PQ ವು ಸಿಲಿಂಡರಿನ ಎತ್ತರ BQ (AP=BQ) ಗಳು ವೃತ್ತಾಕಾರದ ಮೇಲ್ಮೈಗಳ ತ್ರಿಜ್ಯಗಳು..

ನೇರ ಸಿಲಿಂಡರಿನ ಲಕ್ಷಣಗಳು:

1. ಇವುಗಳಿಗೆ ಎರಡು ವೃತ್ತಾಕಾರದ(ಮೇಲೆ ಮತ್ತು ಕೆಳಗೆ) ಸಮತಲಗಳಿವೆ. 2. ಎರಡು ವೃತ್ತಾಕಾರದ ಸಮತಲಗಳು ಪರಸ್ಪರ ಸಮಾಂತರ ಮತ್ತು ಸರ್ವಸಮ. 3. ಎರಡು ಸಮತಲ ಮೇಲ್ಮೈಯನ್ನ ಸೇರಿಸುವ ವಕ್ರರೇಖೆಯು ಸಿಲಿಂಡರಿನ ಪಾಶ್ರ್ವ ಮೇಲ್ಮೈ ಆಗಿರುತ್ತದೆ. 4. ಎರಡು ವೃತ್ತಾಕಾರದ ಸಮತಲಗಳ ಕೇಂದ್ರ ಬಿಂದುವನ್ನ ಸೇರಿಸುವ ರೇಖೆಯು ಸಿಲಿಂಡರಿನ ಅಕ್ಷವಾಗಿರುತ್ತದೆ. 5. ವೃತ್ತಪಾದ ಸಿಲಿಂಡರಿನ ಪಾಶ್ರ್ವಮೇಲ್ಮೈಯ ಎಲ್ಲಾ ಬಿಂದುಗಳು ಸಿಲಿಂಡರಿನ ಅಕ್ಷದಿಂದ ಸಮದೂರದಲ್ಲಿ ಇರುತ್ತವೆ. 6. ವೃತ್ತಾಕಾರದ ಸಮತಲಗಳ ತ್ರಿಜ್ಯವು ಆ ಸಿಲಿಂಡರಿನ ತ್ರಿಜ್ಯ ಆಗಿರುತ್ತದೆ. ಈಗ ಮೇಲಿನ ಸಿಲಿಂಡರಿನ ಹೊರ ಪದರವನ್ನ ಕತ್ತರಿಸಿ, ಬಿಡಿಸಿದಾಗ ಚಿತ್ರದಲ್ಲಿ ತೋರಿಸಿದಂತೆ ABCD ಆಯತ ದೊರೆಯುತ್ತದೆ ಈ ಆಯತದ ಅಗಲ = ಸಿಲಿಂಡರಿನ ಉದ್ದ (ಎತ್ತರ) (AB=h). ಆಯತದ ಉದ್ದ = ವೃತ್ತಾಕಾರದ ತಳದ ಸುತ್ತಳತೆ: P =2r ಸಿಲಿಂಡರಿನ ಪಾರ್ಶ್ವ ಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣ = ಆಯತದ ವಿಸ್ತೀರ್ಣ= ಉದ್ದ*ಅಗಲ P*h = 2 r *h =2rh ಸಿಲಿಂಡರಿನ ಪೂರ್ಣ ಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣ = ವೃತ್ತಾಕಾರದ ಒಂದು ಸಮತಲದ (ಮೇಲ್ಭಾಗ) ವಿಸ್ತೀರ್ಣ+ ಪಾರ್ಶ್ವಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣ+ ವೃತ್ತಾಕಾರದ ಇನ್ನೊಂದು ಸಮತಲದ (ಕೆಳಭಾಗ)ವಿಸ್ತೀರ್ಣ = r^2+2rh+r^2 = 2r^2+2rh =2r(r+h) ಚದರ ಮಾನಗಳು

ಲೆಕ್ಕ ಮಾಡಲು ಸುಲಭವಾಗುವಂತೆ ನಾವು =22/7 ಎಂದು(ಅಂದಾಜು) ತೆಗೆದುಕೊಳ್ಳುತ್ತೇವೆ.

6.15.1 ಸಮಸ್ಯೆ 1: ಒಂದು ಭವನದಲ್ಲಿ 3.5 ಎತ್ತರವಿರುವ 12 ಸ್ತಂಭಗಳಿವೆ. ಪ್ರತಿಯೊಂದು ಸ್ತಂಭದ ಪರಿಧಿಯು 50 ಸೆ.ಮಿ. ಆಗಿರುತ್ತದೆ. ಸ್ತಂಭಗಳ ಪಾರ್ಶ್ವಮೇಲ್ಮೈಗಳಿಗೆ ಬಣ್ಣ ಹಚ್ಚಲು ಚ.ಮಿ.ಗೆ 25ರೂ.ನಂತೆ ತಗಲುವ ಖರ್ಚೆಷ್ಟು?

ಪರಿಹಾರ:

ನಾವೀಗ ಲೆಕ್ಕ ಮಾಡಲು ಎಲ್ಲಾ ಅಳತೆಗಳನ್ನ ಮೀಟರ್ ನಲ್ಲಿಯೇ ತೆಗೆದುಕೊಳ್ಳುವಾ. ಸ್ತಂಭದ ಪಾರ್ಶ್ವಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣ = Ph = 0.5*3.5 = 7/4 ಚ.ಮಿ. 12 ಸ್ತಂಭಗಳ ಒಟ್ಟು ಪಾರ್ಶ್ವಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣ = 12*7/4 = 21 ಚ.ಮಿ.. ಬಣ್ಣ ಹಚ್ಚಲು ತಗಲುವ ಖರ್ಚು = (ವಿಸ್ತೀರ್ಣ *ದರ) =21*25 = 525 ರೂ.ಗಳು.

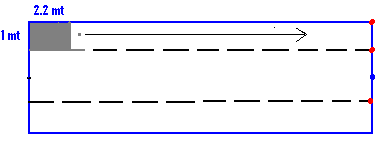
6.15.1 ಸಮಸ್ಯೆ 2: ನಿಮ್ಮ ಶಾಲೆಯ ಆಟದ ಮೈದಾನವನ್ನ ಸಮತಟ್ಟು ಮಾಡಲು 70ಸೆ.ಮಿ. ವ್ಯಾ¸ ಮತ್ತು 1 ಮೀಟರ್ ಉದ್ದದ ರೋಲರನ್ನ ಉಪಯೋಗಿಸಿದೆ. ಆಟದ ಮೈದಾನವನ್ನ ಒಂದು ಬಾರಿ ಕ್ರಮಿಸಲು 200 ಪೂರ್ಣ ಸುತ್ತುಗಳನ್ನ ಹಾಕಿದರೆ, ಮೈದಾನದ ವಿಸ್ತೀರ್ಣ ಎಷ್ಟು?

ಪರಿಹಾರ:

ರೋಲರ್ ನ ತ್ರಿಜ್ಯ = 35 ಸೆ.ಮಿ= 0.35 ಮಿ.( d=2r =70) ರೋಲರ್ ನ ಪಾರ್ಶ್ವಮೇಲ್ಯೈ ವಿಸ್ತೀರ್ಣ = 2rh = 2*(22/7)*.35*1 = 44*.05 = 2.2 ಚ.ಮಿ ರೋಲರ್ 200 ಸುತ್ತು ಹಾಕುವುದರಿಂದ, ಮೈದಾನದ ಒಟ್ಟು ವಿಸ್ತೀರ್ಣ = 200*2.2 = 440 ಚ.ಮಿ.

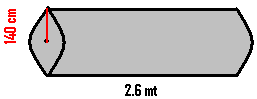
6.15.1 ಸಮಸ್ಯೆ 3: ಒಂದು ಪೆಟ್ರೋಲ್ ಟ್ಯಾಂಕರ್ ನ ಲೋಹದ ಹಾಳೆ ಉಪಯೋಗಿಸಿ ತಯಾರಿಸಲಾಗಿದೆ. ಟ್ಯಾಂಕರಿನ ಉದ್ದ 2.6 ಮೀಟರ್ ಮತ್ತು ಸಿಲಿಂಡರಾಕಾರದ ಟ್ಯಾಂಕರಿನ ತ್ರಿಜ್ಯ 140ಸೆ.ಮಿ. ಆದರೆ ಈ ಟ್ಯಾಂಕರ್ ನ್ನು ತಯಾರಿಸಲು ಎಷ್ಟು ಚದರ ಮೀಟರ್ ಲೋಹದ ಹಾಳೆ ಬೇಕು?

ಪರಿಹಾರ:

ಟ್ಯಾಂಕರ್ ನ ಎಲ್ಲಾ ಬದಿಗಳಲ್ಲಿಯೂ ಮುಚ್ಚಿರುವುದರಿಂದ ನಾವು ಅದರ ಪೂರ್ಣಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣ ಕಂಡುಹಿಡಿಯಬೇಕು ಪೂರ್ಣಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣ = 2r(r+h) = 2*(22/7)*1.4*(1.4+2.6) = 2*22*.2*4 = 35.2 ಚ.ಮಿ.

ಸಿಲಿಂಡರಿನ ಘನಫಲ

ನಮಗೀಗಾಲೇ ತಿಳಿದಿರುವಂತೆ, ಒಂದು ಘನದ ಘನಫಲ = ಉದ್ದ*ಅಗಲ*ಎತ್ತರ =(ತಳದ ವಿಸ್ತೀರ್ಣ)*ಎತ್ತರ ಇದೇ ರೀತಿ ಸಿಲಿಂಡರಿನ ಘನಫಲ = (ವೃತ್ತಾಕಾರದ ಸಮತಲದ ವಿಸ್ತೀರ್ಣ)*ಎತ್ತರ = (r^2)*h = r^2h ಘನಮಾನಗಳು

ನೆನಪಿಡಿ:- ಗಾತ್ರವನ್ನ ಯಾವಾಗಲೂ ಘನಮಾನದಲ್ಲಿಯೇ ಹೇಳಬೇಕು.

6.15.1 ಸಮಸ್ಯೆ 4 ನೀವು ರಸ್ತೆಯಲ್ಲಿ ಹೋಗುವಾಗ ಪೆಟ್ರೋಲ್ ಟ್ಯಾಂಕರ್ನ ನೋಡಿದ್ದೀರಿ. ಅದರ ಸಾಮರ್ಥ್ಯವನ್ನ ಅದರ ಮೇಲೆ ಬರೆದಿರುತ್ತಾರೆ.

ಟ್ಯಾಂಕರಿನ ಸಾಮರ್ಥ್ಯ = ?? ಲೀಟರ್ ಮತ್ತು ಟ್ಯಾಂಕರಿನ ಉದ್ದ = ? ಮೀಟರ್ ಗಳಾದರೆ, ಟ್ಯಾಂಕರಿನ ವ್ಯಾಸವನ್ನ ಮೀಟರ್ ಗಳಲ್ಲಿ ಕಂಡುಹಿಡಿ.

ಅಭ್ಯಾಸ: ಟ್ಯಾಂಕರ್ ನ ಅಳತೆ ತೆಗೆದು ನೀವೇ ಮಾಡಿ

6.15.1 ಸಮಸ್ಯೆ 5: ಒಬ್ಬ ಪೈಂಟ್ ತಯಾರಕನು ಪೈಂಟನ್ನ 14ಸೆ.ಮಿ. ವ್ಯಾಸದ 1 ಲೀಟರ್ ಡಬ್ಬದಲ್ಲಿ ತುಂಬಿಸುತ್ತಾನೆ. ಅವನ ದಾಸ್ತಾನು ಕೋಣೆಯ ಎತ್ತರ 3.245 ಮಿ. ಆದರೆ ಒಂದರ ಮೇಲೆ ಒಂದರಂತೆ ಎಷ್ಟು ಡಬ್ಬಗಳನ್ನ ಜೋಡಿಸಬಹುದು?

ಪರಿಹಾರ:

ಮೊದಲು ನಾವೀಗ ಡಬ್ಬದ ಎತ್ತರವನ್ನ ಕಂಡುಹಿಡಿಯಬೇಕು ಡಬ್ಬದ ವ್ಯಾಸ = 14 ಸೆ.ಮಿ. ತ್ರಿಜ್ಯ = 7 ಸೆ.ಮಿ. ಡಬ್ಬದ ಗಾತ್ರ = r^2h = (22/7)7*7*h = 154h ಡಬ್ಬದ ಗಾತ್ರ 1 ಲೀಟರ್ ಎಂದು ಕೊಟ್ಟಿದೆ. 1 ಲೀಟರ್ = 1000 ಘ.ಸೆ.ಮಿ. 154h =1000h =6.49 ಸೆ.ಮಿ. ದಾಸ್ತಾನು ಕೋಣೆಯ ಎತ್ತರ = 3.245 ಮಿ. ಒಂದರ ಮೇಲೆ ಒಂದು ಇಡ ಬಹುದಾದ ಡಬ್ಬಗಳು =3.245*100/6.49 = 50

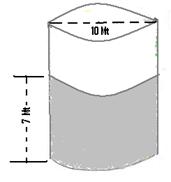
6.15.1 ಸಮಸ್ಯೆ 6: ಒಂದು ವೃತ್ತಾಕಾರದ ಬಾವಿಯಲ್ಲಿ 7 ಮಿ. ಎತ್ತರದವರೆಗೆ ನೀರು ಸಂಗ್ರಹವಾಗಿದೆ. ಬಾವಿಯ ವ್ಯಾಸ 10 ಮಿ. ಇದ್ದರೆ, ಬಾವಿಯಲ್ಲಿ ಸಂಗ್ರಹವಾದ ನೀರಿನ ಪ್ರಮಾಣ ಎಷ್ಟು

ಪರಿಹಾರ:

ಬಾವಿಯ ವ್ಯಾಸ 10 ಮಿ. ಅದರ ತ್ರಿಜ್ಯ = r = 5 ಮಿ. ನೀರಿನ ಗಾತ್ರ = r^2h = (22/7)*5^2*7 = 22*25 = 550 ಘ.ಮಿ. = 5, 50,000 ಲೀಟರ್ ( 1 ಘ.ಮಿ.= = 100*100*100 ಘ.ಸೆ.ಮಿ., 1000 ಘ.ಸೆ.ಮಿ., = 1 ಲೀಟರ್)

6.15.2 ಶಂಕು (Circular cones):

ಶಂಕುವಿನ ಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣ (Surface Area of Cone)

ಧಾನ್ಯದ ರಾಶಿ, ಮರಳಿನ ರಾಶಿ, ಐಸ್ಕ್ರೀಂ ಕಪ್ ಇತ್ಯಾದಿಗಳು ಶಂಕುವಿನ ಪರಿಕಲ್ಪನೆ ಮೂಡಿಸುತ್ತವೆ.

ಸಿಲಿಂಡರ್ ನಂತೆ ಇಲ್ಲಿಯೂ ಕೂಡಾ ನಾವು ಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣ ಮತ್ತು ಘನಫಲಗಳನ್ನ ಕಂಡುಹಿಡಿಯುವ ಕ್ರಮಗಳನ್ನ ನೋಡುವಾ.

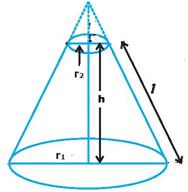
ಪಕ್ಕದ ಚಿತ್ರದಲ್ಲಿ ಶಂಕುವನ್ನ ತೋರಿಸಿದೆ.

ಶಂಕುವಿನ ಲಕ್ಷಣಗಳು:

1. ಶಂಕುವು ಒಂದೇ ಒಂದು ವೃತ್ತಾಕಾರದ ಸಮತಲವನ್ನ ಹೊಂದಿದ್ದು, ಅದರ ತ್ರಿಜ್ಯ = OC =r 2. ಶಂಕುವಿನ ಅಕ್ಷ (A) ಮತ್ತು ಓರೆ ಎತ್ತರ (AC) ಸಂಧಿಸುವ ಬಿಂದುವೇ ಶೃಂಗ ಬಿಂದು A (CA=l) 3. ಪಾದದ ಕೇಂದ್ರ ಬಿಂದುವನ್ನ ಶೃಂಗಕ್ಕೆ ಸೇರಿಸುವ ರೇಖೆಯು ಶಂಕುವಿನ ಎತ್ತರ (OA=h) 4. ಪಾದದ ವೃತ್ತಾಕಾರದ ಅಂಚನ್ನ ಶೃಂಗ ಬಿಂದುವಿಗೆ ಸೇರಿಸುವ ವಕ್ರ ಮೇಲ್ಮೈಯು ಶಂಕುವಿನ ಪಾರ್ಶ್ವಮೇಲ್ಮೈ ಆಗಿರುತ್ತದೆ.

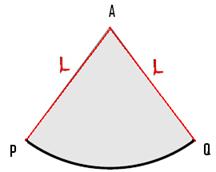
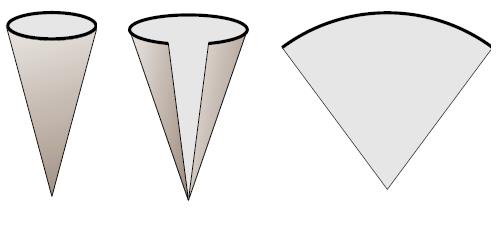
ಒಂದು ಶಂಕುವನ್ನ ನೇರವಾಗಿ ಕೆಳಗಿನ ಚಿತ್ರದಲ್ಲಿ ತೋರಿಸಿದಂತೆ ಕತ್ತರಿಸಿ ಬಿಡಿಸಿದರೆ, ನಮಗೆ ಒಂದು ವೃತ್ತ ಖಂಡ ಸಿಗುತ್ತದೆ.

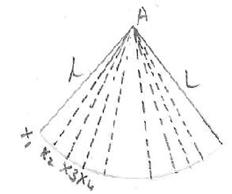
ಎಡಗಡೆ ಚಿತ್ರದಲ್ಲಿನ APQ ಶಂಕುವಿನ ಓರೆ ಎತ್ತರ (l) ದಷ್ಟು ತ್ರಿಜ್ಯದಿಂದ ಎಳೆದ ವೃತ್ತ ಖಂಡಗಳನ್ನು ಬಲಗಡೆ ಚಿತ್ರದಲ್ಲಿಕೊಡಲಾಗಿದೆ.. APQ ಶಂಕುವು, ಅತೀ ಚಿಕ್ಕ ತ್ರಿಕೋನಗಳನ್ನು (AX1X2, AX2X3,,AX3X4, …..) ಒಟ್ಟು ಸೇರಿಸಿದಾಗ ಉಂಟಾದುದುಎಂದೂ ಭಾವಿಸಬಹುದು. X1X2, X2X3, X3X4 ಗಳು ಸರಳರೇಖೆಗಳಲ್ಲದಿದ್ದರೂ APQ ವನ್ನ ಅತೀ ಚಿಕ್ಕ ಚಿಕ್ಕ ಭಾಗಗಳನ್ನಾಗಿ ಮಾಡಿದಾಗ ಅವುಗಳನ್ನ ಸರಳರೇಖೆಗಳೆಂದೇ ಕಲ್ಪಿಸಬಹುದು. ಆಗ ಅವುಗಳು ತ್ರಿಕೋನಗಳ ಪಾದಗಳಾಗುತ್ತವೆ AX1X2 ದ ವಿಸ್ತೀರ್ಣ = (1/2) *ಪಾದ*ಎತ್ತರ =(1/2*ಪಾದ *l ಶಂಕುವಿನ ಪಾರ್ಶ್ವಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣ = ಚಿಕ್ಕ ಚಿಕ್ಕ ತ್ರಿಕೋನಗಳ ವಿಸ್ತೀರ್ಣಗಳ ಮೊತ್ತ = (1/2)*B1l +(1/2)*B2l+(1/2)*B3l+ …….+(1/2)*B1l= (1/2)l [B1+ B2+ B3+ ………+ Bn] ಆದರೆ [B1+ B2+ B3+ ………+ Bn] = ಶಂಕುವಿನ ಪಾದದ ಸುತ್ತಳತೆ = 2r ಶಂಕುವಿನ ಪಾರ್ಶ್ವಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣ =(1/2) l *2r= rl ಶಂಕುವಿನ ಪೂರ್ಣ ಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣ = ವೃತ್ತ ಪಾದದ ವಿಸ್ತೀರ್ಣ+ ಪಾರ್ಶ್ವಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣ = r^2 +rl=r(r+l)

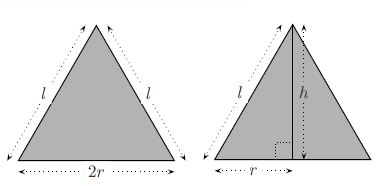
ಶಂಕುವಿನಲ್ಲಿ ಪಾದ, ಎತ್ತರ ಮತ್ತು ಓರೆ ಎತ್ತರಗಳಿರುವ ಸಂಬಂಧ:

ಬಲಬದಿಯ ಚಿತ್ರವನ್ನ ಗಮನಿಸಿ. ಶಂಕುವಿನ ಪಾದದ ತ್ರಿಜ್ಯ = r ಆಗಿರಲಿ. ಶಂಕುವಿನ ಎತ್ತರ = h ಆಗಿರಲಿ. ಓರೆ ಎತ್ತರ = l ಆಗಿರಲಿ ಪೈಥಾಗೊರಸನ ಪ್ರಮೇಯದಿಂದ, l^2= h^2+r^2

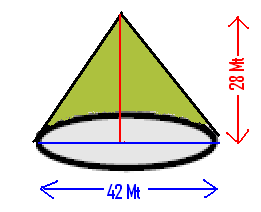
6.15.2 ಸಮಸ್ಯೆ 1: ಶಂಕುವಿನಾಕೃತಿಯ ಡೇರೆಯನ್ನು ಮಧ್ಯದಲ್ಲಿ 28 ಮೀಟರ್ ಕಂಬದಿಂದ ಆಧರಿಸಿ ರಚಿಸಲಾಗಿದೆ. ಡೇರೆಯ ತಳದ ವ್ಯಾಸ 42 ಮೀಟರ್ ಇದ್ದರೆ, ಚ.ಮಿ.ಗೆ 20ರೂ.ನಂತೆ ಡೇರೆಗೆ ಬಳಸಿದ ಕ್ಯಾನ್ವಾಸ್ ಬಟ್ಟೆಯ ಬೆಲೆಯನ್ನ ಕಂಡುಹಿಡಿಯಿರಿ.

ಪರಿಹಾರ:

ಇಲ್ಲಿ r=21 ಮಿ.( d=2r =42): h=28 ನಾವೀಗ ಪಾರ್ಶ್ವಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣ ನೋಡಬೇಕಾಗಿದೆ. ಅದಕ್ಕೆ ನಮಗೆ ಡೇರೆಯ ಓರೆ ಎತ್ತರ ಬೇಕು. ಓರೆ ಎತ್ತರವು ಪಾದದ ತ್ರಿಜ್ಯವು ಪಾದವಾಗಿದ್ದು ಎತ್ತರವು ಇನ್ನೊಂದು ಬಾಹುವಾಗಿರುವ ಲಂಬಕೋನ ತ್ರಿಕೋನದ ವಿಕರ್ಣವಾಗಿರುತ್ತದೆ. ಪೈಥಾಗೊರಸನ ಪ್ರಮೇಯದಂತೆ,( ವಿಕರ್ಣ)^2= (ಪಾದ)^2+( ಪಾದ)^2= (21)^2+(28)^2= 441+784 =1225 =(35)^2 ಓರೆಎತ್ತರ = l = 35 ಮೀಟರ್ ಡೇರೆಯ ಪಾರ್ಶ್ವಮೇಲ್ಯೈ ವಿಸ್ತೀರ್ಣ =rl =(22/7)*21*35 = 22*3*35 =2310 ಚ.ಮಿ. ಕ್ಯಾನ್ವಾಸ್ ಬಟ್ಟೆಯ ಬೆಲೆ = ವಿಸ್ತೀರ್ಣ*ದರ = 2310*20 = 46,200 ರೂ.ಗಳು

6.15.2 ಸಮಸ್ಯೆ: ಪಾದದ ವ್ಯಾಸ 12 ಮೀಟರ್, ಓರೆ ಎತ್ತರ 8 ಮೀಟರ್ ಇರುವಂತೆ ಒಂದು ಶಂಕುವಿನಾಕಾರದ ಗೋಪುರವನ್ನ ಲೋಹದ ಹಾಳೆ ಉಪಯೋಗಿಸಿ ಮಾಡಲು ಒಂದು ಕಾರ್ಖಾನೆಗೆ ತಿಳಿಸಲಾಯಿತು. ಇದಕ್ಕೆ ಬೇಕಾಗುವ ಲೋಹದ ಹಾಳೆಯ ವಿಸ್ತೀರ್ಣ ಕಂಡುಹಿಡಿ.

ಪರಿಹಾರ:

ಇಲ್ಲಿ r=6( d=2r =12), l=8 ಶಂಕುವಿನ ಪೂರ್ಣಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣ =r(r+l) = (22/7)*6*(6+8) = (22/7)*6*14 = 22*6*2 =264 ಚ.ಮಿಟರ್

ಶಂಕುವಿನ ಘನಫಲ (ಗಾತ್ರ) (Volume of Cone):

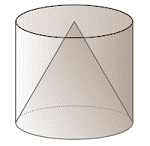
ಪರೀಕ್ಷೆ ಮತ್ತು ಅಳತೆಗಳಿಂದ ನಮಗೆ ತಿಳಿದು ಬರುವ ವಿಷಯವೇನೆಂದರೆ, ಒಂದು ಸಿಲಿಂಡರ್ ಮತ್ತು ಒಂದು ಶಂಕು ಇವುಗಳು ಒಂದೇ ಸಮನಾದ ವೃತ್ತ ಪಾದವನ್ನ ಹೊಂದಿದ್ದು ಒಂದೇ ಎತ್ತರದವುಗಳಾಗಿದ್ದರೆ, ಸಿಲಿಂಡರಿನ ಘನಫಲ ಶಂಕುವಿನ ಘನಫಲ ಮೂರರಷ್ಟಿರುತ್ತದೆ. ಶಂಕುವಿನ ಘನಫಲ = (1/3)* ಸಿಲಿಂಡರಿನ ಘನಫಲ = (1/3)* (r^2)h ಘನ ಮಾನಗಳು ( ಸಿಲಿಂಡರ್ ನ ಗಾತ್ರ =r^2h) = (1/3)* ಪಾದದ ವಿಸ್ತೀರ್ಣ)*h

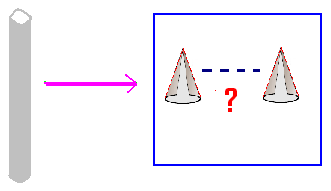
6.15.2 ಸಮಸ್ಯೆ 3: ಒಬ್ಬ ಕಾರ್ಖಾನೆಯ ಕೆಲಸಗಾರನಿಗೆ 3.5ಸೆ.ಮಿ. ತ್ರಿಜ್ಯವಿರುವ ಒಂದು ಮೀಟರ್ ಉದ್ದದ ಸಿಲಿಂಡರಾಕಾರದ ಲೋಹದ ಕಡ್ಡಿಯನ್ನ ಕೊಡಲಾಗಿದೆ. ಅವನು ಅದನ್ನ ಕರಗಿಸಿ, 1ಸೆ.ಮಿ. ತ್ರಿಜ್ಯದ, 2.1 ಸೆ.ಮಿ. ಎತ್ತರದ ಶಂಕುವಿನಾಕೃತಿಗಳನ್ನ ಮಾಡಬೇಕಾಗಿದೆ. ಅವನು ಎಷ್ಟು ಶಂಕುಗಳನ್ನ ಮಾಡಬಲ್ಲ?

ಪರಿಹಾರ:

ಸಿಲಿಂಡರಾಕಾರದ ಕಡ್ಡಿಯ ತ್ರಿಜ್ಯ = r=3.5 ಸೆ.ಮಿ. ಎತ್ತರ (ಉದ್ದ) h=100 ಸೆ.ಮಿ. ಸಿಲಿಂಡರಿನ ಘನಫಲ = r^2h = (22/7)*3.5*3.5*100 = 22*3.5*.5*100 =3850 ಘ.ಸೆ.ಮಿ. ಸಿಲಿಂಡರ್ ನ ಕರಗಿಸಿ ಮಾಡಬೇಕಾದ ಶಂಕುವಿನ ಅಳತೆ (ಇಲ್ಲಿ r=1, h=2.1) ಆಗಿದೆ. ತಯಾರಿಸಬೇಕಾದ ಶಂಕುವಿನ ಘನಫಲ = (1/3)* r^2h = (1/3)*(22/7)*1*1*2.1 = 22*.1 =2.2 ಘ.ಸೆ.ಮಿ. ತಯಾರಿಸಬಲ್ಲ ಶಂಕುಗಳು = (ಕರಗಿಸಿದ ಲೋಹದ ಗಾತ್ರ)/ಶಂಕುವಿನ ಗಾತ್ರ = 3850/2.2 = 1750

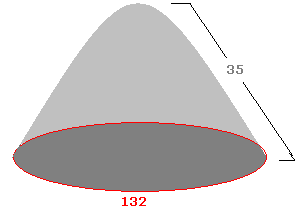
6.15.2 ಸಮಸ್ಯೆ 4: ಒಬ್ಬ ರೈತನು ತಾನು ಬೆಳೆದ ಧಾನ್ಯವನ್ನ ಒಂದು ರಾಶಿ ಹಾಕಿದನು. ಆ ರಾಶಿಯ ಓರೆ ಎತ್ತರ 35 ಅಡಿ. ತಳದ ಸುತ್ತಳತೆ 132 ಅಡಿ. ಅವನು ಧಾನ್ಯವನ್ನ ಅದರ ಗಾತ್ರಕ್ಕನುಗುಣವಾಗಿ ಮಾರಿದರೆ. ಆ ರಾಶಿಯ ಆಕಾರ ಮತ್ತು ಅದರ ಗಾತ್ರ ಕಂಡುಹಿಡಿ.

ಪರಿಹಾರ:

ರಾಶಿಯ ಆಕಾರ ಶಂಕು ಆಕಾರವಾಗಿರುತ್ತದೆ. ಈಗ ಈ ಶಂಕು ಆಕೃತಿಯ ರಾಶಿಯ ಗಾತ್ರ (ಘನಫಲ) ಕಂಡುಹಿಡಿಯಬೇಕಾಗಿದೆ. ತಳದ ಸುತ್ತಳತೆ ಮತ್ತು ರಾಶಿಯ ಓರೆ ಎತ್ತರ ಕೊಟ್ಟಿದ್ದಾರೆ. ಘನಫಲವನ್ನ ಕಂಡುಹಿಡಿಯಲು ನಮಗೆ ತ್ರಿಜ್ಯ ಮತ್ತು ಎತ್ತರ ಬೇಕು. ಸುತ್ತಳತೆ (ಪರಿಧಿ) = 2r r = (ಸುತ್ತಳತೆ)/ 2 = 132*7/(2*22) = 3*7 = 21 ಅಡಿ ಓರೆ ಎತ್ತರ: l^2=h^2- r^2 h^2=l^2- r^2= (35)^2-(21)^2= 1225-784=441 =(28)^2 ಎತ್ತರ = h = 28 ಅಡಿ ಎತ್ತರ = (1/3)* (r^2)h = (1/3)*(22/7)*21*21*28= 22*21*28 = 12,936 ಘನ ಅಡಿಗಳು

ತಲೆಕೆಳಗೆ ಮಾಡಿದ ಬಕೆಟ್ ಆಕಾರದ ವಸ್ತುವಿನ(ಶಂಕುವಿನ ಭಿನ್ನಕದ) ವಿಸ್ತೀರ್ಣ ಮತ್ತು ಘನಫಲ:

ಶಂಕುವಿನ ಮೇಲ್ಭಾಗದಿಂದ ಇನ್ನೊಂದು ಚಿಕ್ಕ ಶಂಕುವಾಗುವಂತೆ ಭಾಗ ಮಾಡಿದರೆ ಉಂಟಾಗುವ ಎರಡು ಶಂಕುಗಳ ತಳದ ತ್ರಿಜ್ಯ, ಎತ್ತರ ಮತ್ತು ಓರೆ ಎತ್ತರಗಳು ಸಮಾನುಪಾತದಲ್ಲಿ ಇರುತ್ತವೆ.

ಚಿತ್ರ 1 ಚಿತ್ರ 2

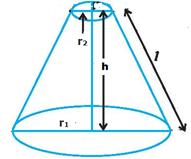
ಮೊದಲನೇ ಚಿತ್ರದಲ್ಲಿನ ಶಂಕುವಿನ ತ್ರಿಜ್ಯ r₁ ಆಗಿದೆ. ಈ ಶಂಕುವನ್ನು ತಳಕ್ಕೆ ಸಮಾನಾಂತರವಾಗಿ ಮಧ್ಯಭಾಗದಲ್ಲಿ ಕತ್ತರಿಸಿದಾಗ ದೊರೆಯುವುದೇ ಚಿತ್ರ 2 ರಲ್ಲಿ ಕಾಣಿಸಿರುವಂತಹ ಆಕೃತಿ. ಅದೇ ಶಂಕುವಿನ ಭಿನ್ನಕ. ಭಿನ್ನಕದ ಎತ್ತರ h, ಓರೆ ಎತ್ತರ l ,ತಳದ ತ್ರಿಜ್ಯ r₁ ,ಮತ್ತು ಮೇಲ್ಭಾಗದ ತ್ರಿಜ್ಯ r₂ ಆದರೆ ಆಗ:

l=

ಶಂಕುವಿನ ಭಿನ್ನಕದ ಘನಫಲ = h(r₁²+ r₂²+ r₁r₂)

ಶಂಕುವಿನ ಭಿನ್ನಕದ ಪಾರ್ಶ್ವ ಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣ = l(r₁ + r₂)

ಶಂಕುವಿನ ಭಿನ್ನಕದ ಪೂರ್ಣ ಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣ = [ l(r₁ + r₂) + (r₁²+ r₂²)]

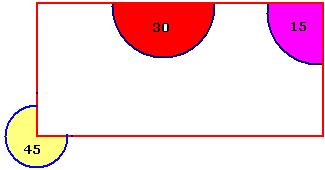
6.15.2 ಸಮಸ್ಯೆ 5: ಗೋಡೆಯ ಪಕ್ಕದಲ್ಲಿರುವ ಧಾನ್ಯ ರಾಶಿಯ ಪರಿಧಿ 30, ಒಳ ಕೋನದಲ್ಲಿರುವ ರಾಶಿಯದು 15, ಹೊರಗಡೆ 45 ಹಸ್ತ ಗಳಾಗಿದ್ದು ಎತ್ತರ 6 ಹಸ್ತಗಳಾದರೆ ಅವುಗಳ ಗಾತ್ರಗಳನ್ನು ಹೇಳು(ಲೀಲಾವತಿ ಶ್ಲೋಕ 237)

ಪರಿಹಾರ:

ರಾಶಿಯ ಆಕಾರ ಶಂಕು ಆಕಾರವಾಗಿರುತ್ತದೆ. ಹಸ್ತ ಎಂದರೆ ಅಳತೆಯ ಮಾನ, (ಅಂದಾಜಾಗಿ ಒಂದುವರೆ ಅಡಿ)

ಧಾನ್ಯದ ರಾಶಿಗಳ ಪಾದ ವೃತ್ತದ ಭಾಗವಾಗಿದ್ದು ಅವುಗಳ ತ್ರಿಜ್ಯ ಕಂಡು ಹಿಡಿಯಬೇಕು.ಅವು ಎಲ್ಲವೂ 60 ಹಸ್ತ ಪರಿಧಿ ಇರುವ ವೃತ್ತದ ಅರ್ಧ, ಕಾಲು ಮತ್ತು ಮುಕ್ಕಾಲು ಪಾದವನ್ನು ಹೊಂದಿವೆ ಎನ್ನುವುದನ್ನು ಗಮನಿಸಿ. 2r = 60 , =3 ಆದರೆ, r = 60/6 = 10 ಶಂಕುವಿನ ಘನಫಲ = (1/3)* (ಪಾದದ ವಿಸ್ತೀರ್ಣ)*h: ಎತ್ತರ =6 30 ಪರಿಧಿ ಇರುವ ರಾಶಿಯ ಗಾತ್ರ = {1/2}*(1/3)*(r^2)*h= (1/6)*3*10^2*6 = 300 15 ಪರಿಧಿ ಇರುವ ರಾಶಿಯ ಗಾತ್ರ = {1/4}*(1/3)*(r^2)*h= (1/12)*3*10^2*6 = 150 45 ಪರಿಧಿ ಇರುವ ರಾಶಿಯ ಗಾತ್ರ = {3/4}*(1/3)*(r^2)*h= (3/12)*3*10^2*6 = 450

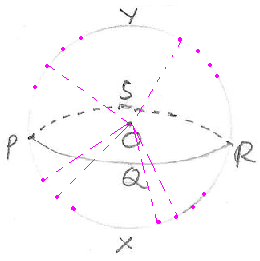
6.15.3 ಗೋಳ(Sphere)

ಕಾಲ್ಚೆಂಡು, ಕ್ರಿಕೆಟ್ ಬಾಲ್, ಕಬ್ಬಿಣದ ಗುಂಡು ಇವೆಲ್ಲಾ ಗೋಳಗಳಿಗೆ ಉದಾಹರಣೆಗಳು.

ಗೋಳದ ಲಕ್ಷಣಗಳು:

1. ಗೋಳದಲ್ಲಿ ಒಂದು ಕೇಂದ್ರ(O)ವಿದೆ. 2. ಗೋಳದ ಮೇಲ್ಮೈಯ ಮೇಲಿನ ಎಲ್ಲಾ ಬಿಂದುಗಳೂ ಕೇಂದ್ರದಿಂದ ಒಂದೇ ದೂರದಲ್ಲಿವೆ. 3. ಈ ಸಮಾನ ದೂರವೇ ಗೋಳದ ತ್ರಿಜ್ಯವಾಗಿದೆ. 4. ಕೇಂದ್ರದ ಮೂಲಕ ಹಾದು ಹೋಗುವ ಒಂದು ಸಮತಲವು ಗೋಳವನ್ನ ಎರಡು ಸಮಭಾಗಗಳಾಗಿ ವಿಭಾಗಿಸುತ್ತದೆ. ಪ್ರತಿಯೊಂದು ಭಾಗವೂ ಅರ್ಧಗೋಳ.

ಗೋಳದ ಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣ (Surface area of sphere):

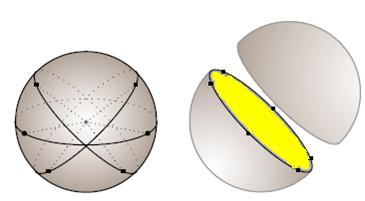
ಪರೀಕ್ಷೆಗಳಿಂದ ಮತ್ತು ಅಳತೆಗಳಿಂದ ನಾವು ತೀರ್ಮಾನಿಸಬಹುದೇನೆಂದರೆ, ಒಂದುಗೋಳದ ಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣವು ಗೋಳದ ವ್ಯಾಸದ ಮೂಲಕ ಹಾದು ಹೋಗುವ ವೃತ್ತಾಕಾರದ(ಚಿತ್ರದಲ್ಲಿ ಹಳದಿ ಬಣ್ಣ) ಸಮತಲದ ವಿಸ್ತೀರ್ಣದ ನಾಲ್ಕರಷ್ಟಿರುತ್ತದೆ ಗೋಳದ ಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣ = 4 r^2 ಚ.ಮಾನಗಳು (ವೃತ್ತಾಕಾರದ ಸಮತಲದ ವಿಸ್ತೀರ್ಣ = ವೃತ್ತದ ವಿಸ್ತೀರ್ಣ = r^2)

ಕುತೂಹಲದ ವಿಷಯವೇನೆಂದರೆ, ಒಂದು ಗೋಳದ ಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣವು ಆ ಗೋಳವು ಹಿಡಿಸಲ್ಪಡುವ ಸಿಲಿಂಡರಿನ ಪಾರ್ಶ್ವಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣಕ್ಕೆ ಸಮ. (ಚಿತ್ರ ನೋಡಿ) ಸಿಲಿಂಡರಿನ ಪಾರ್ಶ್ವ ಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣ =2rh = 2r*2r = 4 r^2 ( 6.15.1 ನೋಡಿ) (ಸಿಲಿಂಡರ್ ನ ಎತ್ತರ = h = ಗೋಳದ ವ್ಯಾಸ = 2r)

6.15.3 ಸಮಸ್ಯೆ 1: ಒಂದು ಅರ್ಧ ಗೋಳಾಕಾರದ ಗೊಮ್ಮಟದ ಪಾದದ ಸುತ್ತಳತೆ 44 ಮೀಟರ್ ಇದೆ. ಇದಕ್ಕೆ ಬಣ್ಣ ಹಚ್ಚಲು ಚ.ಮಿ.ಗೆ ರೂ.200 ರಂತೆ ಎಷ್ಟು ಹಣ ಬೇಕಾಗುತ್ತದೆ?

ಪರಿಹಾರ:

ಸುತ್ತಳತೆ(ಪರಿಧಿ) = 2r r = ಸುತ್ತಳತೆ(ಪರಿಧಿ) /2 = (1/2)*44*(7/22) = 7 ಮಿ. ಗೋಳದ ಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣ(ಚಿತ್ರದಲ್ಲಿ ಮೇಲಿನ ಭಾಗ) = 4r^2 = 4*(22/7)*7*7 = 4*22*1*7 = 616 ಚ.ಮಿ ಅರ್ಧ ಗೋಳದ ಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣ = ½ * ಗೋಳದ ಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣ = 308 ಚ.ಮಿ ಬಣ್ಣ ಹಚ್ಚಲು ಬೇಕಾದ ಹಣ = ವಿಸ್ತೀರ್ಣ *ದರ = 308*200 = 61,600 ಚ.ಮಿ.

ಗೋಳದ ಘನಫಲ (ಗಾತ್ರ)(Volume of sphere):

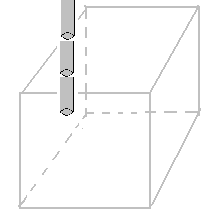
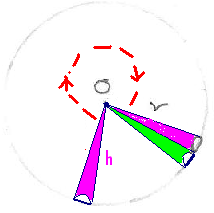
ವಿಟಮಿನ್ A, C , ಕಬ್ಬಿಣ ಮತ್ತು ಕ್ಯಾಲ್ಯಿಯಂಗಳಿಂದ ಸಮೃದ್ಧವಾದ ಕಲ್ಲಂಗಡಿ ಹಣ್ಣನ್ನು ಯಾರು ತಾನೆ ನೋಡಿಲ್ಲ? ವ್ಯಾಪಾರಿಯು ನಿಮಗೆ ಹಣ್ಣನ್ನ ಮಾರುವ ಮೊದಲು ಅದರ ಪರೀಕ್ಷೆಗಾಗಿ, ಅದನ್ನ ಹೇಗೆ ಕತ್ತರಿಸಿ, ಚೂರನ್ನ ಹೊರತೆಗೆಯುತ್ತಾನೆಂದು ಗಮನಿಸಿದ್ದೀರಾ? ಅವನು ಮೊದಲು ಚೂರಿಯನ್ನು ಹಣ್ಣಿನೊಳಗೆ ತೂರಿಸಿ, ತಿರುಗಿಸಿ, ಚೂರನ್ನ ತೆಗೆಯುತ್ತಾನೆ.(ಚಿತ್ರ ನೊಡಿ) ಇದೇ ತತ್ವವನ್ನ ಗೋಳಕ್ಕೂ ಅನ್ವಯಿಸುವಾ

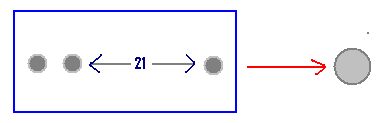
ಗೋಳವನ್ನ ಅದರ ತ್ರಿಜ್ಯದಷ್ಟೇ ಎತ್ತರವುಳ್ಳ, ವೃತ್ತಾಕಾರದ ಪಾದವುಳ್ಳ ಚಿಕ್ಕ ಚಿಕ್ಕ ಶಂಕುಗಳನ್ನ ಒಟ್ಟು ಸೇರಿಸಿ ಮಾಡಿದ್ದು ಎಂದು ಪರಿಗಣಿಸಬಹುದು. (ಬದಿಯಲ್ಲಿನ ಚಿತ್ರ ನೋಡಿ) ನಮಗೆ ಈಗಲೇ ತಿಳಿದಿರುವಂತೆ, ಶಂಕುವಿನ ಘನಫಲ = 1/3 (ಶಂಕುವಿನ ವೃತ್ತ ಪಾದದ ವಿಸ್ತೀರ್ಣ)*ಎತ್ತರ 1 ನೇ ಶಂಕುವಿನ ಘನಫಲ = 1/3 B1r 2 ನೇ ಶಂಕುವಿನ ಘನಫಲ = 1/3 B2r … n ನೇ ಶಂಕುವಿನ ಘನಫಲ 1/3 Bnr ಗೋಳದ ಘನಫಲ = ಶಂಕುವಿನ ಘನಫಲದ ಮೊತ್ತ = (1/3) B1r+(1/3) B2r.......... (1/3) Bnr = (1/3)*r(B1+B2.......... +Bn) = (1/3)*r**(ಗೋಳದ ಮೇಲ್ಯೈ ವಿಸ್ತೀರ್ಣ) (ಚಿಕ್ಕ ಶಂಕುಗಳ ಪಾದಗಳನ್ನ ಸೇರಿಸಿದಾಗ ಗೋಳದ ಹೊರಮೈ ಸಿಗುವುದು) = (1/3)*r*4r^2 = 4/3 r^3(ಗೋಳದ ಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣ = 4r^2)

ಗಮನಿಸಿ: ಚಿತ್ರದಲ್ಲಿ ತೋರಿಸಿದಂತೆ, ಒಂದು ಶಂಕುವನ್ನ ಒಂದು ಗೋಳದಲ್ಲಿ ತೂರಿಸಿದರೆ, ಗೋಳದ ಘನಫಲವು ಶಂಕುವಿನ ಘನಫಲದ ನಾಲ್ಕರಷ್ಟಿರುತ್ತದೆ

6.15.3 ಸಮಸ್ಯೆ 2: ಒಂದು ಸಿಹಿತಿಂಡಿ ಮಾಡುವ ಅಂಗಡಿಯಲ್ಲಿ ಅಳತೆಗಾಗಿ 14 ಸೆ.ಮಿ. ತ್ರಿಜ್ಯವಿರುವ ಅರ್ಧ ಗೋಳಾಕಾರದ ಬಟ್ಟಲನ್ನ ಉಪಯೋಗಿಸುತ್ತಾರೆ. ಅದರಲ್ಲಿ ಹಿಡಿಸುವ ತುಪ್ಪದ ಪ್ರಮಾಣವನ್ನ ಲೀಟರಿನಲ್ಲಿ ಕಂಡುಹಿಡಿ.

ಪರಿಹಾರ:

ಇಲ್ಲಿ r = 21 ಸೆ.ಮಿ. ಗಮನಿಸಿ: ಅರ್ಧಗೋಳ = ಗೋಳದ ಅರ್ಧ ಭಾಗ ಅರ್ಧಗೋಳಾಕಾರದ ಬಟ್ಟಲಿನ ಘನಫಲ = 2/3 r^3= 2/3 *22/7*14*14*14 = 5749.3 ಘ.ಸೆ.ಮಿ = 5.75 ಲೀಟರ್ ( 1000 ಘ.ಸೆ.ಮಿ.= 1 ಲೀಟರ್)

6.15.3 ಸಮಸ್ಯೆ 3: ಒಂದೇ ಗಾತ್ರವಿರುವ 2ಸೆ.ಮಿ. ತ್ರಿಜ್ಯವಿರುವ 21 ಸೀಸದ ಗೋಲಿಗಳನ್ನ ಕರಗಿಸಿ, ಒಂದು ದೊಡ್ಡ ಗೋಳವನ್ನ ತಯಾರಿಸಲಾಗಿದೆ.

ಆ ಗೋಳದ ತ್ರಿಜ್ಯ ಮತ್ತು ಘನಫಲ ಕಂಡುಹಿಡಿ.

ಪರಿಹಾರ:

1 ಗೋಲಿಯ ಘನಫಲ 4/3 r^3= (4/3)*(22/7)*2*2*2 = 32*22/21 21 ಗೋಲಿಯ ಘನಫಲ 21*32*22/21 = 32*22 = 704 ಘ.ಸೆ.ಮಿ ಈ ಗೋಲಿಗಳನ್ನ ಕರಗಿಸಿ ದೊಡ್ಡ ಗೋಳ ತಯಾರಿಸಿದೆ. ದೊಡ್ಡ ಗೋಳದ ಘನಫಲ 704ಘ.ಸೆ.ಮಿ. ಗೋಳದ ಘನಫಲ = 4/3 r^3=(4/3)*(22/7)r^3 = 88/21r^3= 704 r^3 = 704*(21/88) =168 r =5.52 ಸೆ.ಮಿ. (ಕ್ಯಾಲ್ಕುಲೇಟರ್ ಉಪಯೋಗಿಸಿದೆ) ತಾಳೆ: 5.52 ಸೆ.ಮಿ. ಗೋಳದ ಘನಫಲ 4/3 r^3= (4/3)*(22/7)*5.52*5.52*5.52 = 704

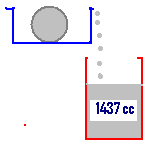
6.15.3 ಸಮಸ್ಯೆ 4 : ಒಂದು ಕಬ್ಬಿಣದ ಶಾಟ್ಪುಟ್ ಬಾಲನ್ನ ನೀರು ತುಂಬಿದ ಜಾಡಿಯಲ್ಲಿ ಮುಳುಗಿಸಿದಾಗ, ಅದು 1437ಘ.ಸೆ.ಮಿ. ನೀರನ್ನ ಹೊರಚೆಲ್ಲಿತು. ಹಾಗಾದರೆ ಆ ಬಾಲಿನ ವ್ಯಾಸ ಕಂಡುಹಿಡಿ.

ಪರಿಹಾರ:

ಶಾಟ್ಪುಟ್ ನ ಘನ ಫಲ = 1437cc4/3 r^3=1437cc i,e (4/3)*(22/7)r^3 =1437 r^3 = 1437*21/(4*22) =343 r=7 ಸೆ.ಮಿ. ಶಾಟ್ಪುಟ್ ಬಾಲಿನ ವ್ಯಾಸ = 14 ಸೆ.ಮಿ. ತಾಳೆ: ಶಾಟ್ಪುಟ್ ಬಾಲ್ ನ ಘನಫಲ = 4/3 r^3 = (4/3)*(22/7)*7*7*7 = (4/3)*22*7*7 =1437

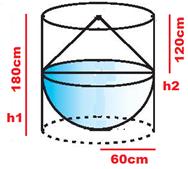
6.15 ಸಮಸ್ಯೆ 5: 60 cm ತ್ರಿಜ್ಯವಿರುವ ಅರ್ಧಗೋಳದ ಪಾದದ ಮೇಲೆ 120 cm ಎತ್ತರ ಮತ್ತು 60 cm ತ್ರಿಜ್ಯವನ್ನು ಹೊಂದಿರುವ ನೇರ ವೃತ್ತಪಾದ ಶಂಕುವನ್ನು ಜೋಡಿಸಲಾಗಿದೆ. ಸಂಪೂರ್ಣವಾಗಿ ನೀರಿನಿಂದ ತುಂಬಿದ ನೇರ ವೃತ್ತಪಾದ ಸಿಲಿಂಡರಿನಲ್ಲಿ ತಳವನ್ನು ಮುಟ್ಟುವಂತೆ ನೇರವಾಗಿ ಈ ಘನಾಕೃತಿಯನ್ನು ಮುಳುಗಿಸಲಾಗಿದೆ. ಸಿಲಿಂಡರಿನ ತ್ರಿಜ್ಯವು 60 cm ಮತ್ತು ಎತ್ತರವು 180 cm ಆದರೆ ಸಿಲಿಂಡರಿನಲ್ಲಿ ಉಳಿದಿರುವ ನೀರಿನ ಪ್ರಮಾಣವನ್ನು ಕಂಡುಹಿಡಿ.ಘನ ಮೀ

ಪರಿಹಾರ:

ಸಿಲಿಂಡರಿನ ತ್ರಿಜ್ಯ =ಗೋಳದ ತ್ರಿಜ್ಯ = ಶಂಕುವಿನ ತ್ರಿಜ್ಯ = 60 cm=r ಸಿಲಿಂಡರಿನ ಎತ್ತರ = h1= 180 cm ; ಶಂಕುವಿನ ಎತ್ತರ =h2=120 cm ಸಿಲಿಂಡರಿನಲ್ಲಿ ಉಳಿದ ನೀರು = ಸಿಲಿಂಡರಿನ ಘನಫಲ – ಗೋಳದ ಘನಫಲ - ಶಂಕುವಿನ ಘನಫಲ = r^2h1 - r^3-r^2h2 = r^2(h1- r -h2) = r^2( 180- *60 -*120) = *60*60*(180-40-40) = *60*60*100= *10000 113*10000 ಘನ ಸೆಂ.ಮೀ = 1.13 ಘನ ಮೀ.

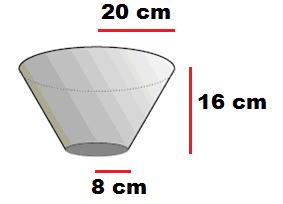
6.15 ಸಮಸ್ಯೆ 6: ಒಂದು ಲೋಹದ ಹಾಳೆಯಿಂದ ಮಾಡಿದ ಮತ್ತು ಮೇಲ್ಭಾಗದಲ್ಲಿ ತೆರೆದಿರುವ ಒಂದು ಪಾತ್ರೆಯು ಶಂಕುವಿನ ಭಿನ್ನಕದ ಆಕಾರದಲ್ಲಿ ಇದೆ. ಶಂಕುವಿನ ಭಿನ್ನಕದ ಎತ್ತರ 16 cm. ಅದರ ಕೆಳಭಾಗದ ಮತ್ತು ಮೇಲ್ಭಾಗದ ತ್ರಿಜ್ಯಗಳು ಕ್ರಮವಾಗಿ 8 cm ಹಾಗೂ 20 cm ಕ್ರಮವಾಗಿ ಇದೆ. ಈ ಪಾತ್ರೆಯನ್ನು ಹಾಲಿನಿಂದ ಸಂಪೂರ್ಣವಾಗಿ ತುಂಬಿಸಬೇಕಾಗಿದೆ. 1 ಲೀಟರ್ ಹಾಲಿನ ಬೆಲೆಯು ರೂ 20 ರಂತೆ ಆದರೆ ಹಾಲನ್ನು ಕೊಳ್ಳಲು ಎಷ್ಟು ಹಣ ಬೇಕು? ಲೋಹದ ಹಾಳೆಯ ದರ ಪ್ರತಿ 100 cm² ಗೆ ರೂ 8 ಆದರೆ ಇಡೀ ಪಾತ್ರೆಯನ್ನು ನಿರ್ಮಿಸಲು ಎಷ್ಟು ಹಣ ಬೇಕಾಗುತ್ತದೆ? ( = 3.14 ಎಂದು ಅಂದಾಜಿಸಿ).

ಪರಿಹಾರ:

ಪಾತ್ರೆಯ ಒಂದು ಕರಡು ಚಿತ್ರ ರಚಿಸಿ. ಇಲ್ಲಿ h=16, r1= 8 ಮತ್ತು r2=20 l== = 20 ಪಾತ್ರೆಯ ಘನಫಲ =h(r1^2+ r2^2+ r1r2) =*3.14*16(20^2+ 8^2+ 20*8)= *3.14*16*(624) = 3.14*16*208 10449 cc=10.449 ಲೀಟರ್ ಹಾಲಿನ ಬೆಲೆ 10.449*20 209 ರೂ
ಪಾತ್ರೆಯ ಸಂಪೂರ್ಣ ಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣ = ಶಂಕು ಭಿನ್ನಕದ ಪಾರ್ಶ್ವ ಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣ + ಪಾತ್ರೆಯ ತಳದ ವಿಸ್ತೀರ್ಣ = l(r1 + r2)+ r1^2 = [ l(r1 + r2) + r1^2 ] =3.14[ 20*28+64] = 3.14*624= 1959.36 ಚ. ಸೆ.ಮೀ. ಲೋಹದ ಹಾಳೆಯ ಬೆಲೆ= 1959.36*8* ರೂ 156

6.15 ಕಲಿತ ಸಾರಾಂಶ

l, b, h ಗಳು ಒಂದು ಆಯತ ಘನದ ಉದ್ದ, ಅಗಲ, ಎತ್ತರಗಳನ್ನು ಸೂಚಿಸಿದರೆ,a ಯು ಘನದ ಒಂದು ಬದಿಯನ್ನು ಸೂಚಿಸಿದರೆ, h ಮತ್ತು l ಗಳು ಎತ್ತರ ಮತ್ತು ಓರೆ ಎತ್ತರಗಳನ್ನೂ, r ತ್ರಿಜ್ಯವನ್ನು ಸೂಚಿಸಿದರೆ: