8.3: Heights and distances (Solution of Right Triangles):

In this section we learn methods of finding values of remaining sides and angles when we are given:

1. Two sides of the triangle.

2. One side and one interior (standard) angle of the triangle.

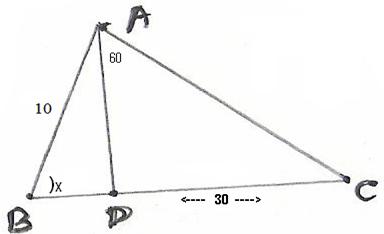
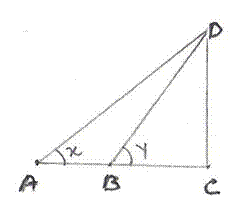
8.3 Problem 1: Find sin x in the below mentioned figure.

Solution:

tan60= (= Opposite Side /Adjacent Side) DC/AD = 30/AD = AD = 30/ sin x = Opposite Side /Hypot. = AD/AB = (30/)/10 = 3/ = Thus sin x =

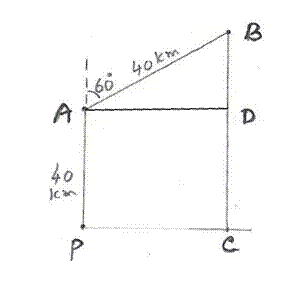
8.3 Problem 2: In the figure given below, a rocket is fired vertically upwards from its launching pad P. It first rises 40km vertically and then travels 40km at 60⁰ to the vertical.

PA represents the first stage of the journey and AB the second. C is a point vertically below B on the horizontal level as P.

Calculate:

(!) The height of the rocket from the ground when it is at point B

(!!) The horizontal distance of point C from P.

Solution:

Since PA is parallel to CB CD = 40km and ABD = 60^0(Alternate angles) Hence BAD =30^0 Cos 60 = Adjacent Side /Hyp. = BD/AB = BD/40 We know cos 60 = 1/2 1/2 = BD/40 Thus BD =20 sin 60 = Opposite Side /Hyp. = AD/AB Since sin 60 = /2 We have /2 = AD/40 AD = 20 = 20*1.732 = 34.64 km= CP BC = BD+CD= 20+40 = 60km

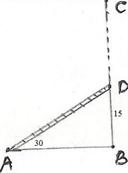
8.3 Problem 3: A ladder is placed against a vertical tower. If the ladder makes an angle of 30⁰ with the ground and reaches up to a height of 15m of the tower,

find the length of the ladder. This angle is called 'Angle of elevation'.

(The angle of elevation is the angle made by the object to the horizontal line (could be imaginary in some problems) to the ground, as seen by observer looks up at the object).Hence this angle is formed above the horizontal line.

Solution:

It is given that BD=15 and DAB = 30^0 Sin 30 = sin DAB = Opposite Side /Hyp. = BD/AD = 15/AD We know sin 30 = 1/2 1/2 = 15/AD AD = 30m

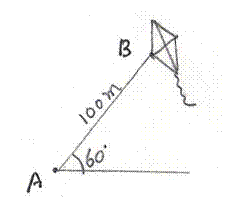
8.3 Problem 4: A kite is attached to a 100m long string. Find the greatest height reached by the kite, when the string makes an angle of 60⁰ (the Angle of elevation)with the level ground.

Solution:

We know Sin 60 = Opposite Side /Hyp. = Max height/100 We also know sin 60 = /2 Max height/100 = /2 Thus Max height = 100/2 = 50 = 50*1.732 = 86.6 m

8.3 Problem 5: If tan x = 5/12, tan y = 3/4 and AB = 48m find the length of CD

Solution:

tan x = Opposite Side /Adjacent Side = DC/AC tan y = Opposite Side /Adjacent Side = DC/BC tanx/tan y =(DC/AC)/ (DC/BC ) = (DC/AC) *(BC/DC)= BC/AC By substituting given values for tanx and tan y we get tan x/tan y=(5/12)/(3/4) = (5/12)*(4/3) = 5/9 BC/AC = 5/9 I.e. 9BC = 5AC Since AC=AB+BC, 5AC = 5(AB+BC) = 5AB+5BC 9BC = 5AB+5BC I.e. 4BC= 5AB = 5*48 = 240 BC = 60m tan y = Perp/Adjacent Side = DC/BC = DC/60 But it is given that tan y = 3/4 Hence 3/4 = DC/60 DC = (3/4)*60 = 45M

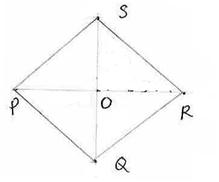
8.3 Problem 6: The perimeter of a rhombus is 96cm and obtuse angle of it is 120⁰. Find the length of its diagonals

Solution:

Since in a rhombus all sides are equal :PQ = 96/4 = 24cm Let PQR = 120^0 We also know that in rhombus diagonals bisect each other perpendicularly and diagonals bisect the angle at vertex. Hence POR is a right angled triangle and PQO = 1/2(PQR) = 60^0 Sin 60 = Opposite Side /Hyp. = PO/PQ = PO/24 /2 = PO/24 (sin 60 = /2 ) PO = 12 = 12*1.732 = 20.784 PR = 2PO = 2*20.784 = 41.568cm cos 60 = Adjacent Side /Hyp. = OQ/24 1/2=OQ/24 (cos 60 = 1/2) QO = 24 /2 =12 QS = 2QO = 2*12 = 24cm

QS = 2QO = 2*12 = 24cm

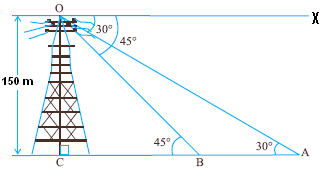
8.3 Problem 7: As observed from the top of 150M tall light house, the angles of depression of two ships approaching it are 30⁰ and 45⁰

If one ship is behind the other, find the distance between the two ships.

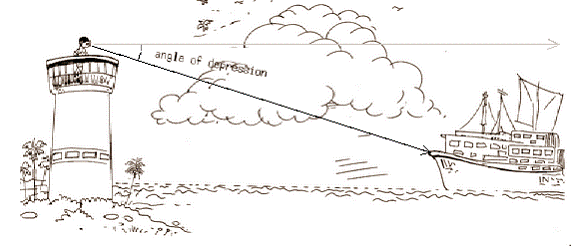
(The angle of depression is the angle made by the imaginary horizontal line to the ground from the top of light house to the ship, as seen by observer sitting in the light house).

The angle of depression is the angle made by the observer to the horizontal line (could be imaginary in some problems) to the ground, when observer looks down at the object. Hence this angle is formed below the horizontal line.

Solution:

In the adjoining figure CO can be imagined to be light house of height 150m. B and A are the position of ships. XOA is the angle of depression of the ship A which is given to be 30^0 XOB is the angle of depression of the ship B which is given to be 45^0 Since OX is parallel to the ground It follows that OAC = 30^0 OBC = 45^0 OC is the opposite side =150 BC/150= Cot 45 = 1 (Cot 45 = 1) BC =150 AC/150= Cot 30 = (Cot 30 = ) AC =150 AB(Distance between ships) = AC-BC = 150 -150 = 150(-1) = 109.8(Approximate)

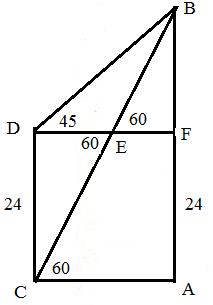
8.3 Problem 8: The angles of elevation of the top of cliff as seen from the top and bottom of a building are 45⁰ and 60⁰ respectively. If the height of the building is 24M, find the height of the cliff.

Solution:

In the figure CD is building, AB is cliff. we need to find AB In this problem we will be using the value of tan(60^0) Given CD=24M, FDA =45^0 ,ACB= 60^0 Construction: DF is an imaginary line drawn parallel to the ground which cuts CB at E BF = DF ( BDF is an isosceles right angled triangle) = DE + EF = 24/+EF (DEC = 60^0 and tan(60^0)= = DC/DE and DC=24) = 24/+BF/ (BEF = 60^0 and = tan(60^0) = BF/EF ) BF = 24+BF ( Multiply both sides by ) BF = 24/(-1) AB= AF+ BF = 24 + 24/(-1) = 24{1+1/(-1)} =24* /(-1)

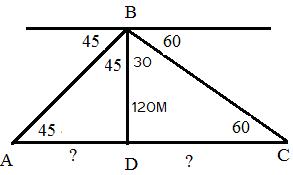
8.3 Problem 9: from a light house the angles of depression of 2 ships on opposite sides of the light house were observed to be 45⁰ and 60⁰ . If the height of the light house is 120M and the line joining the 2 ships passes through the foot of the light house, find the distance between 2 ships

Solution:

In the figure DB is light house. A and C are positions of 2 ships. Given: BD=120M, DBA =45^0 ,DBC= 60^0 Construction: AC is a line that joins ship A and C passing through D which is the Adjacent Side of Light house AD = DB=120 ( ABD is an isosceles right angled triangle) AC =AD+DC =120+DC =120+120/(DBC = 60^0 and tan(60^0) = = DB/DC and DB=120) =120+ 120*/3= 120+40.

8.3 Summary of learning

No	Points studied
1	Finding of angles and sides of distance objects