8.4 ತ್ರಿಕೋನಮಿತಿಯ ನಿತ್ಯ ಸಮೀಕರಣಗಳು

 

8.4.1 ಮೂಲ ಸಂಬಂಧಗಳು

ಈ ಹಿಂದೆ ಕಲಿತಂತೆ:

 

sin

ಅಭಿಮುಖ ಬಾಹು/ವಿಕರ್ಣ

=; Cosec ==

 

 

 

cos

ಪಾರ್ಶ್ವ ಬಾಹು/ವಿಕರ್ಣ

=; sec = =

tan

ಅಭಿಮುಖ ಬಾಹು/ಪಾರ್ಶ್ವ ಬಾಹು  =  

=; cot = =

 

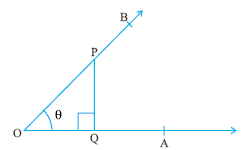
ಪೈಥಾಗೊರಸ್ ಪ್ರಮೇಯದಂತೆ PQ2 + OQ2 = OP2   -----à(1)

 +  = 1(ಎರಡೂ ಕಡೆ  OP2 ನಿಂದ ಭಾಗಿಸಿದೆ)

()2 + ()2 = 1 (sin)2 + (cos)2 = 1                      sin2 + cos2 = 1         ----------(I)

ಸಮೀಕರಣ (1) ನ್ನು  ಎರಡೂ ಕಡೆ  OQ2 ನಿಂದ ಭಾಗಿಸಿದಾಗ

 + 1 =  ()2 + 1 = ()2

1 + (tan)2 = (sec)2                                              tan2 + 1 = sec2          --------(II)

ಸಮೀಕರಣ (1) ನ್ನು  ಎರಡೂ ಕಡೆ  PQ2 ನಿಂದ ಭಾಗಿಸಿದಾಗ

1 + =   1 + ()2 = ()2

1 + (cot)2 = (cosec)2                                              1 + cot2 = cosec2     --------(III)

ಸಮೀಕರಣ  (I), (II) ಮತ್ತು  (III) ನ್ನು   ಮೂಲ ಸಂಬಂಧಗಳು ಎನ್ನುತ್ತೇವೆ..

 

               

 

 

 

 

                

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ಮೊದಲನೇ ಮೂಲ ಸಂಬಂಧವನ್ನು ಆಧರಿಸಿ ಈ ಕೆಳಗಿನ ಸಂಬಂಧಗಳನ್ನೂ ಪಡೆಯಬಹುದು.

1.   sin2= 1-cos2  sin = (1-cos2)

2.   cos2= 1-sin2  cos = (1- sin2)

 ಲಘುಕೋನವಾದಾಗ   sin  ಮತ್ತು   cos ಗಳು ಧನವಾಗಿರುತ್ತವೆ. ಆಗ

sin = +(1-cos2) 

cos = +(1-sin2)

ಮೂಲ ಸಂಬಂಧಗಳನ್ನು ಉಪಯೋಗಿಸಿ  ಈ ಕೆಳಗಿನ ಸಂಬಂಧಗಳನ್ನೂ ಪಡೆಯಬಹುದು. :

1.   tan = +(sec2-1),

2.   sec = +(1+tan2),

3.   cot = +(cosec2-1),

4.   cosec = +(1+cot2)

tan =  =

 

 

 

 

 

 

 

 

 

 

 

 

ವಿವಿಧ  ಸಂಬಂಧಗಳನ್ನು ಕೆಳೆಗೆ ನೀಡಿದಂತೆ ಕ್ರೋಢೀಕರಿಸಬಹುದು:

 

ಗಮನಿಸಿ :   sin2+cos2=1 ಎನ್ನುವ ಒಂದೇ ಸಂಬಂಧದಿಂದ ಕೆಳಗೆ ನಮೂದಿಸಿರುವ ಎಲ್ಲಾ ಸಂಬಂಧಗಳನ್ನು  ಪಡೆಯಬಹುದು

\pm {\frac {\sqrt {1-\cos ^{2}\theta }}{\cos \theta }}\!

 

 

8.4 ಸಮಸ್ಯೆ 1:  (1+x2)*sin = x ಆದರೆ,  + = x2 +  ಎಂದು ಸಾಧಿಸಿ.

ಪರಿಹಾರ:

 (1+x2)*sin = x (ದತ್ತ)     sin =      sin2 =  (ವರ್ಗೀಕರಿಸಿದೆ)   --------(1)

 cos2 = 1 - sin2 (sin2+cos2=1, ಪಕ್ಷಾಂತರದಿಂದ)

            = 1 -    = =                                                       --------(2)

(1) ಮತ್ತು (2) ರಿಂದ

                          =  = x2                                                      ---------(3)

                       =                                                                   ---------(4)

(3) ಮತ್ತು (4) ರಿಂದ

                          + = x2 +

 

8.4 ಸಮಸ್ಯೆ 2: sin6+cos6=1-3*sin2.cos2 ಎಂದು ಸಾಧಿಸಿ.

ಪರಿಹಾರ:

x = sin2 ಮತ್ತು y = cos2 ಆಗಿರಲಿ.

x+y = 1  (sin2+cos2=1)

 LHS ಭಾಗವು  a3+b3 ರೂಪದಲ್ಲಿದೆ, ಅದರ ಸೂತ್ರವನ್ನು ಉಪಯೋಗಿಸಿದಾಗ

             x3+y3 = (x+y)3-3xy(x+y) = 1-3xy(x+y =1)

                                                       = 1 – 3*sin2.cos2

8.4 ಸಮಸ್ಯೆ 3: + = 2cosecA ಎಂದು ಸಾಧಿಸಿ.

 

ಪರಿಹಾರ:

LHS = ( ಛೇದ (secA+1)*(secA-1) ಆಗಿರುವಂತೆ)

=  (sec2-1 = tan2)

=

= (tanA =)

=  (cosA = )

= 2cosecA

8.4.2 ಪೂರಕ ಕೋನಗಳ ತ್ರಿಕೋನಮಿತಿಯ ಅನುಪಾತಗಳು

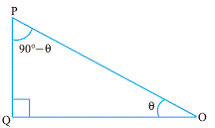
ಲಂಬಕೋನ ತ್ರಿಕೋನದಲ್ಲಿ   ಒಂದು ಲಘುಕೋನವಾಗಿದ್ದರೆ, ಇನ್ನೊಂದು ಕೋನ 900- ಆಗಿರಲೇ ಬೇಕು( ತ್ರಿಕೋನದಲ್ಲಿ ಎಲ್ಲಾ ಕೋನಗಳ ಮೊತ್ತ 1800).

 

 ಪಕ್ಕದ ಚಿತ್ರದಲ್ಲಿ, QOP =   QPO = 900-

         sin =    ----à(1)

         cos =    ----à(2)

         tan =    ----à(3)

QPO ನ್ನು ಪರಿಶೀಲಿಸಿದಾಗ

cos(900-) =     --à (4)

sin(900-) =     ---à(5)

cot(900-) =   ---à(6)

 (1), (2) ಮತ್ತು (3) ಗಳನ್ನು   (4), (5) ಮತ್ತು (6)  ರ ಜೊತೆಗೆ ಹೋಲಿಸಿದಾಗ :   

    

1

sin = cos(900-)

2

cos = sin(900-)

3

tan= cot(900-)

4

cosec = sec(900-)

5

sec = cosec(900-)

6

cot= tan(900-)

 

 

 

 

 

 

 

8.4 ಸಮಸ್ಯೆ 4: 3 - = ?

 

ಪರಿಹಾರ:

28 = 90-62 ಮತ್ತು 48 = 90-42 ಆಗಿರುವುದರಿಂದ

cos(28) = cos(90-62) = sin62

ie. cosec(48) = cosec(90-42) = sec(42)

 3 -

   = 3-

  = 3-1 = 2

 

8.4 ಸಮಸ್ಯೆ 5: sec4A=Cosec(A-200) ಆಗಿದ್ದು  4A ಲಘುಕೋನವಾಗಿದ್ದರೆ  A ಎಷ್ಟು?

 

ಪರಿಹಾರ:

ನಮಗೆ  sin ಮತ್ತು cos ಗಳು ಹೆಚ್ಚು ಪರಿಚಿತವಾಗಿರುವುದರಿಂದ  ಮೇಲಿನ ಸಮೀಕರಣದ ವಿಲೋಮವನ್ನು ಪರಿಗಣಿಸುವ.

=

Ie,  cos4A= sin(A-200)

sin(90-4A)= sin(A-200) (  4A ಲಘುಕೋನವಾಗಿರುವುದರಿಂದ  cos = sin(900-))

 90-4A= A-200

 90+20= A+4A

 110= 5A

 A= 220

 

 

8.4. ಕಲಿತ ಸಾರಾಂಶ 

 

ಕ್ರ.ಸಂ.

ಕಲಿತ ಮುಖ್ಯಾಂಶಗಳು

1

sin2+cos2=1, tan2 + 1 = sec2, 1 + cot2 = cosec2

2

ಪೂರಕ ಕೋನಗಳ ತ್ರಿಕೋನಮಿತಿಯ ಅನುಪಾತಗಳು