1.3 ಘನಗಳು ಮತ್ತು ಘನಮೂಲಗಳು (Cubes and Cube roots):

 

 

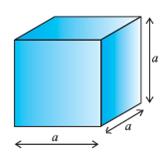
ಘನ ಎಂದಾಗ ನೆನಪಾಗುವುದು ಉದ್ದ ಅಗಲ ಮತ್ತು ಎತ್ತರ  ಎನ್ನುವ  3 ಅಳತೆ ಪ್ರಮಾಣಗಳಲ್ಲಿ ಎಲ್ಲವೂ ಸಮವಾಗಿರುವ (ಉದ್ದ = ಅಗಲ = ಎತ್ತರ) ಬದಿಯಲ್ಲಿನ ಆಕೃತಿಯಂತಹ ವಸ್ತು.

ಒಂದು ಘನಾಕೃತಿಯ ಗಾತ್ರ(ಘನ ಫಲ) = ಉದ್ದ*ಅಗಲ*ಎತ್ತರ.( ರೇಖಾಗಣಿತದಲ್ಲಿ ಕಲಿತಿದ್ದೇವೆ.)

ಒಂದು ಘನವು ಸಮಾನ ಉದ್ದ, ಅಗಲ, ಎತ್ತರಗಳನ್ನು ಹೊಂದಿರುತ್ತದೆ.

ಒಂದು ಘನದ ಗಾತ್ರ(ಘನ ಫಲ) = ಉದ್ದ * ಉದ್ದ * ಉದ್ದ = (ಉದ್ದ)3

ಇಲ್ಲಿ a ಯು 1,2,3 ಆದಾಗ ಅದರ ಘನ ಫಲ ಕ್ರಮವಾಗಿ 1*1*1 = 1,  2*2*2=8, 3*3*3=27 ಆಗುತ್ತದೆ.

 

1, 2, 3, 4…  ಗಳ ಗುಂಪಿಗೂ ಮತ್ತು 1, 8, 27, 64 . . . ಗುಂಪಿಗೂ ಇರುವ  ಸಂಬಂಧ ಏನು?

ಮೊದಲ ಗುಂಪಿನಲ್ಲಿ ಇರುವ  ಸಂಖ್ಯೆಯನ್ನು ಅದರಿಂದಲೇ ಮೂರು ಬಾರಿ ಗುಣಿಸಿದಾಗ ಎರಡನೇ ಗುಂಪಿನ ಸಂಖ್ಯೆಗಳು ದೊರಕಿದವು.  ಇವುಗಳನ್ನು ಘನಗಳೆನ್ನುತ್ತೇವೆ.

ಘನ ಸಂಖ್ಯೆಗಳು ಯಾವುದೇ ಸಂಖ್ಯೆಯನ್ನು 3 ರ ಘಾತಕ್ಕೆ ಏರಿಸಿದ ಸಂಖ್ಯೆಗಳು. ಇವು n3 ರೂಪದಲ್ಲಿವೆ.

n3 ಎಂಬುದು n ನ ಘನವಾದರೆ (cube), n ಎಂಬುದು n3  ದ ಘನಮೂಲ cube root). ಘನಮೂಲವನ್ನು ಸಂಕೇತದಿಂದ ಸೂಚಿಸುತ್ತೇವೆ.

ಆದ್ದರಿಂದ, 1,2,3,4 ಈ ಸಂಖ್ಯೆಗಳು ಕ್ರಮವಾಗಿ 1, 8, 27, 64 ರ ಘನಗಳು.

 

ವ್ಯಾಖ್ಯೆ: ಸರ್ವಸಮವಾದ ಮೂರು ಅಪವರ್ತನಗಳ ಗುಣಲಬ್ಧವಾಗಿರುವ ಯಾವುದೇ ಸಂಖ್ಯೆಯನ್ನು ಆ ಅಪವರ್ತನದ ಘನ(cube) ಎಂದು ಕರೆಯುತ್ತೇವೆ..

 

1.3 ಸಮಸ್ಯೆ 1 : ಒಂದು ಘನದ ಒಂದು ಬದಿಯ ಉದ್ದ  7 ಸೆಂ.ಮಿ. ಆದರೆ ಅದರ ಗಾತ್ರ ಕಂಡುಹಿಡಿ..

 

ಪರಿಹಾರ:

ಘನದ ಗಾತ್ರ = (ಉದ್ದ)3

 7 ಸೆಂ.ಮಿ. ಅಂಚುಳ್ಳ ಘನದ ಗಾತ್ರ = (7)3

=7*7*7 = 343 ಘನ ಸೆಂ.ಮಿ.

 

1.3.1 ಅಪವರ್ತನ ವಿಧಾನದಿಂದ ಘನಮೂಲವನ್ನು  ಕಂಡುಹಿಡಿಯುವುದು(Finding cube root by factorization):

 

1.3.1 ಸಮಸ್ಯೆ 1 : 42875 ರ ಘನಮೂಲ ಕಂಡುಹಿಡಿ.

 

ಪರಿಹಾರ:

42875 ರ ಅಪವರ್ತನಗಳು: 5,5,5,7,7,7                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                       

 42875 = 5*5*5*7*7*7 = 53*73= (5*7)3

 = 5*7 = 35

 

1.3.1 ಸಮಸ್ಯೆ 2: 432 ನ್ನ ಒಂದು ಪೂರ್ಣ ಘನ ಸಂಖ್ಯೆಯನ್ನಾಗಿ ಮಾಡಲು ಅದಕ್ಕೆ ಗುಣಿಸಬೇಕಾದ ಅಥವಾ ಭಾಗಿಸಬೇಕಾದ ಕನಿಷ್ಟ ಸಂಖ್ಯೆ ಕಂಡುಹಿಡಿ.

 

ಪರಿಹಾರ:

432  = 3,3,3,4.4 = (3)3*(4)2

ಇಲ್ಲಿ ಅಪವರ್ತನ ‘4’ ಎರಡೇ ಬಾರಿ ಬಂದಿದೆ.

1. ಈಗ ನಾವು 432 ನ್ನು 4 ರಿಂದ ಗುಣಿಸಿದರೆ, 432*4 = (3)3*(4)3= (3*4)3  ಬರುತ್ತದೆ.

ಆದ್ದರಿಂದ 432 ನ್ನು 4 ರಿಂದ ಗುಣಿಸಿದಾಗ ಅದು ಒಂದು ಪೂರ್ಣಘನ  (1728) ಆಗುತ್ತದೆ.

2. ಈಗ ನಾವು  432 ನ್ನು  16 ರಿಂದ ಭಾಗಿಸಿದರೆ, 432/16= 33 ಬರುತ್ತದೆ.

ಆದ್ದರಿಂದ 432 ನ್ನು  16 ರಿಂದ ಭಾಗಿಸಿದಾಗ , ಅದು ಪೂರ್ಣಘನ (27) = 33 ಆಗುತ್ತದೆ.

 

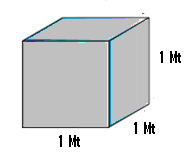
1.3.1  ಸಮಸ್ಯೆ 3: ಒಂದು ಘನ ಸೆಂಟಿಮೀಟರ್ ನೀರು 1 ಗ್ರಾಂ ತೂಗಿದರೆ, ಒಂದು ಘನ ಮೀಟರ್ ನೀರಿನ ತೂಕವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.

 

ಪರಿಹಾರ:

1 ಮೀಟರ್ = 100  ಸೆಂ.ಮೀ.

1 ಘನ ಮೀಟರ್ = 1 ಮೀ.*1 ಮೀ.*1 ಮೀ. = 100 ಸೆಂ.ಮೀ.*100 ಸೆಂ.ಮೀ.* 100 ಸೆಂ.ಮೀ.

= 1000000 ಘನ ಸೆಂ.ಮೀ.

1 ಘನ ಸೆಂ.ಮೀ ನೀರಿನ ತೂಕ= 1 ಗ್ರಾಂ

1 ಘನ  ಮೀ. ನೀರಿನ ತೂಕ = 1000000 ಘನ ಸೆಂ.ಮೀ. ನೀರಿನ ತೂಕ= 1000000 ಗ್ರಾಂ  

= 1000 ಕಿ.. ಗ್ರಾಂ

 

1.3 ಕಲಿತ ಸಾರಾಂಶ

 

 

ಸಂಖ್ಯೆ

ಕಲಿತ ಮುಖ್ಯಾಂಶಗಳು

1

ಘನಗಳು, ಅಪವರ್ತನ ವಿಧಾನದಲ್ಲಿ ಘನಮೂಲವನ್ನು ಕಂಡುಹಿಡಿಯುವುದು.