2.7 ರೇಖಾತ್ಮಕ
ಸಮೀಕರಣಗಳು (Linear
Equations):
1. ಮೂರು ಅನುಕ್ರಮ ಸಮ ಸಂಖ್ಯೆಗಳ ಮೊತ್ತ 252. ಆದರೆ ಆ ಸಂಖ್ಯೆಗಳಾವುವು? (ಅವು 80,82,84 ? 70,72,74 ?)
2. ಒಂದು ಆಯತದ ಉದ್ದವು ಅಗಲಕ್ಕಿಂತ 4 ಸೆಂ.ಮೀ ಹೆಚ್ಚಿದೆ. ಸುತ್ತಳತೆಯು ಅಗಲಕ್ಕಿಂತ 11ಸೆಂ.ಮೀ. ಹೆಚ್ಚಿದ್ದಲ್ಲಿ ಆಯತದ ಉದ್ದ ಮತ್ತು ಅಗಲಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.(ಉದ್ದ 6, ಅಗಲ 2) ? (ಉದ್ದ 7, ಅಗಲ 3 ? )
3. ಒಬ್ಬ ಯಾತ್ರಿಕನು ತನ್ನ ಹಣದ ಅರ್ಧ ಭಾಗವನ್ನು ಪ್ರಯಾಗದಲ್ಲಿಯೂ, ಉಳಿದುದರ 2/9 ಭಾಗವನ್ನು ಕಾಶಿಯಲ್ಲಿಯೂ, ಉಳಿದುದರ 1/4 ಭಾಗವನ್ನು ತೆರಿಗೆಗಳಿಗೂ, ಇನ್ನುಳಿದುದರ 6/10 ಭಾಗವನ್ನು ಗಯೆಯಲ್ಲಿಯೂ ಖರ್ಚುಮಾಡಿದ ನಂತರ ಉಳಿದ 63 ನಿಷ್ಕಗಳನ್ನು(ಹಣದ ಅಳತೆ) ಮನೆಗೆ ತಂದರೆ, ಯಾತ್ರೆಗೆ ತೆಗೆದು ಕೊಂಡು ಹೋದ ಹಣ ಎಷ್ಟು?(ಲೀಲಾವತಿ ಶ್ಲೋಕ 55)
ಇಂತಹ ಸಮಸ್ಯೆಗಳನ್ನು ಬಿಡಿಸುವುದನ್ನು ಇಲ್ಲಿ ಕಲಿಯುತ್ತೇವೆ.
ವ್ಯಾಖ್ಯೆ: ಎರಡು ಬೀಜೋಕ್ತಿಗಳ ಸಮಾನತೆಯನ್ನು ಸೂಚಿಸುವ ಹೇಳಿಕೆಯನ್ನು ‘ಸಮೀಕರಣ’ (Equations) ಎನ್ನುತ್ತೇವೆ. ಸಮೀಕರಣದಲ್ಲಿ ಬರುವ ಒಂದು ಅಥವಾ ಒಂದಕ್ಕಿಂತ ಹೆಚ್ಚು ಅವ್ಯಕ್ತ ಪದಗಳ ರಾಶಿಯನ್ನು ‘ಚರಾಕ್ಷರ’ಗಳೆನ್ನುವರು.
ಉದಾ:
x+2
=5
ಸಮೀಕರಣದ ಎಡಭಾಗವನ್ನು (LHS) ಎಂತಲೂ ಬಲಭಾಗವನ್ನು (RHS) ಎಂತಲೂ ಹೇಳುತ್ತೇವೆ.
ಗಮನಿಸಿ:
6=6 ಇದು ಸರಿತಾನೆ? ======è (1)
ಇಲ್ಲಿ ಎಡಭಾಗ (LHS) ದಲ್ಲಿ 6 ಇದೆ. ಬಲಭಾಗದಲ್ಲೂ 6 ಇದೆ. ಇವೆರಡೂ ಪರಸ್ಪರ ಸಮ.
ಈಗ 2 ನ್ನು ಸಮೀಕರಣ (1)ರ ಎರಡೂ ಬದಿಗಳಿಗೆ ಕೂಡಿಸುವಾ.
ಎಡಭಾಗ (LHS) =6+2=8 , ಬಲಭಾಗ (RHS) = 6+2 =8
ಈಗಲೂ ಕೂಡಾ ಎರಡೂ ಭಾಗಗಳು ಪರಸ್ಪರ ಸಮ.
ಈಗ ಸಮೀಕರಣ (1) ಎರಡೂ ಬದಿಗಳಿಂದ 3 ನ್ನ ಕಳೆಯುವಾ.
ಎಡಭಾಗ = 6-3 =3 , ಬಲಭಾಗ = 6-3 =3
ಈಗಲೂ ಕೂಡಾ ಎರಡೂ ಭಾಗಗಳು ಸಮ.
ಈಗ ಎರಡೂ ಬದಿಗಳಿಗೆ 6 ರಿಂದ ಗುಣಿಸಿ
ಎಡಭಾಗ = 6*6=36 , ಬಲಭಾಗ = 6*6
=36
ಈಗಲೂ ಎಡಭಾಗ = ಬಲಭಾಗ.
ಸಮೀಕರಣ (1)ರ ಎರಡೂ ಬದಿಗಳನ್ನು 3 ರಿಂದ ಭಾಗಿಸಿ.
ಎಡಭಾಗ = 6/3=2 , ಬಲಭಾಗ = 6/3=2
ಎಡಭಾಗ = ಬಲಭಾಗ.
ಸಮಾನತೆಯ ಗುಣಗಳು(ಸ್ವಯಂ ಸಿದ್ಧಗಳು) (Properties
of Equality):(Axioms)
1. ಒಂದೇ ಪರಿಮಾಣವನ್ನು ಸಮೀಕರಣದ ಎರಡೂ ಬದಿಗಳಿಗೆ ಕೂಡಿಸಿದರೆ, ಸಮಾನತೆ ಬದಲಾಗುವುದಿಲ್ಲ.
2. ಒಂದೇ ಪರಿಮಾಣವನ್ನು ಸಮೀಕರಣದ ಎರಡೂ ಬದಿಗಳಿಗೆ ಕಳೆದರೆ, ಸಮಾನತೆ ಬದಲಾಗುವುದಿಲ್ಲ.
3. ಒಂದೇ ಪರಿಮಾಣದಿಂದ ಸಮೀಕರಣದ ಎರಡೂ ಬದಿಗಳಿಗೆ ಗುಣಿಸಿದರೆ, ಸಮಾನತೆ ಬದಲಾಗುವುದಿಲ್ಲ.
4. ಒಂದೇ ಪರಿಮಾಣದಿಂದ ಸಮೀಕರಣದ ಎರಡೂ ಬದಿಗಳಿಗೆ ಭಾಗಿಸಿದರೆ, ಸಮಾನತೆ ಬದಲಾಗುವುದಿಲ್ಲ
LHS=RHS ಇರುವ ಯಾವುದೇ ಸಮೀಕರಣದಲ್ಲಿ ಮೇಲಿನ ಯಾವುದಾದರೂ ಕ್ರಿಯೆಯನ್ನು ನಡೆಸಿದರೆ,ಫಲಿತಾಂಶವೂ LHS=RHS ಆಗಿರುತ್ತದೆ.
ವ್ಯಾಖ್ಯೆ: ಏಕ ಪರಿಮಾಣಾತ್ಮಕವಿರುವ ಬಹುಪದಗಳಾಗಲೀ, ಮೊದಲನೇ ಘಾತವಿರುವ ಚರಾಕ್ಷರಗಳನ್ನಾಗಲೀ ಹೊಂದಿರುವ ಸಮೀಕರಣಗಳೇ ರೇಖಾತ್ಮಕ ಸಮೀಕರಣಗಳು. (‘linear
equation’)
ಉದಾ:
x+2
=5, 3*(a-5) =6, ½ x -4/5 = 3x+7.
ಆದರೆ x2-4 =0 ಇದು ರೇಖಾತ್ಮಕ ಸಮೀಕರಣವಲ್ಲ (ಏಕೆಂದರೆ x ನ ಘಾತಾಂಕ 2)
ಉದಾಹರಣೆ1:
x-3 = 1 ಈ ಹೇಳಿಕೆಯನ್ನು ಗಮನಿಸಿ. ಇಲ್ಲಿ x ಒಂದು ಚರಾಕ್ಷರ.
ಈ ಹೇಳಿಕೆಯನ್ನ ಹೀಗೂ ಹೇಳಬಹುದು: “xನ ಬೆಲೆಯನ್ನು ಕಂಡು ಹಿಡಿಯಿರಿ- ಹೇಗೆಂದರೆ ಅದರಲ್ಲಿ 3 ನ್ನ ಕಳೆದಾಗ ಫಲಿತಾಂಶ 1 ಆಗಬಹುದು.”
ಈಗ x-3 =1 ಹೇಳಿಕೆಯಲ್ಲಿನ x ಗೆ ಬೇರೆಬೇರೆ ಬೆಲೆಗಳನ್ನು ಆದೇಶಿಸುವಾ.
1. x = 1 ಆಗಲು ಸಾಧ್ಯವೆ? ಇಲ್ಲ. ಏಕೆಂದರೆ 1-3
=-2![]()
2. x = 2 ಆಗಲು ಸಾಧ್ಯವೆ? ಇಲ್ಲ. ಏಕೆಂದರೆ 2-3
=-1![]()
3. x =5 ಆಗಲು ಸಾಧ್ಯವೆ? ಇಲ್ಲ. ಏಕೆಂದರೆ 5-3
=2![]()
4. x =4 ಆಗಲು ಸಾಧ್ಯವೆ? ಹೌದು 4-3=1.
ಈ ರೀತಿಯಲ್ಲಿ xನ ಬೆಲೆ ಕಂಡುಹಿಡಿಯಲು ತುಂಬಾ ಸಮಯಬೇಕು.
ಆದರೆ ಗಣಿತ ಶಾಸ್ತ್ರದಲ್ಲಿ ಇದಕ್ಕೆ ಸುಲಭ ವಿಧಾನವಿದೆ.
ದತ್ತ ಹೇಳಿಕೆಯ ಎರಡೂಬದಿಗೆ 3ನ್ನೇ ಕೂಡಿಸುವಾ.
x-3+3= 1+3
x+0 = 4.
x= 4
ಇಲ್ಲಿ ನಾವೀಗ ಒಂದೇ ಪರಿಮಾಣ(=3)ವನ್ನು ಎರಡೂ ಬದಿಗಳಿಗೆ ಕೂಡಿಸಿದ್ದೇವೆ.
ಕೂಡಿಸಲು 3ನ್ನೇ ಯಾಕೆ ತೆಗೆದು ಕೊಂಡಿದ್ದೇವೆ?
ನಮಗೆ ಎಡಭಾಗದಲ್ಲಿ x ಬಿಟ್ಟು ಉಳಿದ ಯಾವ ಸಂಖ್ಯೆಯೂ ಬೇಡ. ಅದನ್ನು ತೆಗೆಯಲಿಕ್ಕಾಗಿ -3 ನ್ನು ತೆಗೆಯಲು 3 ನ್ನ ಕೂಡಿಸಬೇಕಾಯಿತು
ಉದಾಹರಣೆ 2: 6x+4 = 3x+10 ಆದರೆ x ನ ಬೆಲೆ ಕಂಡುಹಿಡಿಯಿರಿ.
ಇಲ್ಲಿ: 6x+4
ಬಲಭಾಗ: 3x+10
ಹಂತ 1:
3x ನ್ನ ಎರಡೂ ಬದಿಗಳಿಂದ ಕಳೆಯಿರಿ.(ಯಾಕೆಂದರೆ ಬಲಭಾಗದಲ್ಲಿರುವ ಚರಾಕ್ಷರವನ್ನು ತೆಗೆಯಬೇಕು.)
ಬಲಭಾಗ = 3x+10-3x= 10
ಎಡಭಾಗ= 6x+4-3x = 3x+4
2 ನೇ ಸ್ವಯಂಸಿದ್ಧದಿಂದ, ಬಲಭಾಗ= ಎಡಭಾಗ.
ಹಂತ 2:
ಈಗ ಎಡಭಾಗದಲ್ಲಿರುವ 4 ನ್ನ ತೆಗೆಯಬೇಕು.ಆದ್ದರಿಂದ ಎರಡೂಬದಿಗಳಿಂದ 4ನ್ನ ಕಳೆಯಿರಿ
ಎಡಭಾಗ= 3x+4-4=3x
ಬಲಭಾಗ = 10-4 = 6
2 ನೇ ಸ್ವಯಂಸಿದ್ಧದಿಂದ, ಬಲಭಾಗ= ಎಡಭಾಗ.
ಹಂತ 3
ಎಡಭಾಗದ x ನ ಸಹಗುಣಕ 3ರಿಂದ ಎರಡೂ ಬದಿಗಳನ್ನ ಭಾಗಿಸಿ.
ಎಡಭಾಗ= 3x/3 =x
ಬಲಭಾಗ = 6/3 =2
4 ನೇ ಸ್ವಯಂಸಿದ್ಧದಿಂದ, ಬಲಭಾಗ= ಎಡಭಾಗ.
x=2
ಈಗ ಮೊದಲೆರಡು ಹಂತಗಳಲ್ಲಿ ನಾವೇನು ಮಾಡಿದ್ದೇವೆ?
ಮೊದಲು ಎರಡೂ ಬದಿಗಳಿಂದ 3xನ್ನ ಕಳೆದು, ನಂತರ ಸ್ಧಿರಾಂಕ 4ನ್ನ ಕಳೆದಿದ್ದೇವೆ.
ಇದರ ಅರ್ಥ: 3xನ್ನ ಮತ್ತು 4ರ ಸಂಕಲನದ ವಿಲೋಮ (-3x ಮತ್ತು-4) ನ್ನ ಎರಡೂ ಬದಿಗಳಿಗೆ ಕೂಡಿಸಿದ್ದು.
ಅಥವಾ 3x ನ ಚಿಹ್ನೆ ಬದಲಾವಣೆ ಮಾಡಿ, ಇನ್ನೊಂದು ಬದಿಗೆ ಹಾಕಿದ್ದೇವೆ.
ಅದೇರೀತಿ 4 ರ ಚಿಹ್ನೆ ಬದಲಾಯಿಸಿ ಇನ್ನೊಂದು ಬದಿಯಲ್ಲಿ ಬರೆದಿದ್ದೇವೆ.
ಈಗ ಹಂತಗಳನ್ನು ಕ್ರೋಢೀಕರಿಸುವಾ:
|
ಹಂತ |
ಹೇಳಿಕೆ |
ವಿವರಣೆ |
|
1 |
6x+4= 3x+10 |
ದತ್ತ ಸಮೀಕರಣ |
|
2 |
6x+4-3x =10 i.e. 3x+4 =10 |
ಬಲಭಾಗದಿಂದ ಎಡಭಾಗಕ್ಕೆ 3x ಚಿಹ್ನೆ ಬದಲಾಯಿಸಿಕೊಂಡು ಹೋಗಿದೆ.. |
|
3 |
3x= 10-4 i.e. 3x =16 |
4 ಎಡಭಾಗದಿಂದ ಬಲಭಾಗಕ್ಕೆ ಚಿಹ್ನೆ ಬದಲಾಯಿಸಿಕೊಂಡು ಹೋಗಿದೆ. |
|
4 |
x=2 |
ಸುಲಭರೂಪಕ್ಕೆ ತಂದಿದೆ(ಎರಡೂ ಬದಿಯನ್ನು 3 ರಿಂದ ಭಾಗಿಸಿದೆ) |
ತಾಳೆ:
ಸಮೀಕರಣ (1) ರಲ್ಲಿ x ನ ಬದಲಾಗಿ 2 ನ್ನ ಆದೇಶಿಸಿ.
ಎಡಭಾಗ= 6*2+4 = 16
ಬಲಭಾಗ= 3*2+10 =16
ಬಲಭಾಗ= ಎಡಭಾಗ.=16
; x=2 ಇದು ಸರಿಯಾದ ಉತ್ತರ.
ವ್ಯಾಖ್ಯೆ: ಯಾವ ಚರಾಕ್ಷರದ ಬೆಲೆಯನ್ನು ಸಮೀಕರಣದಲ್ಲಿ ಆದೇಶಿಸಿದಾಗ, ಎರಡೂ ಕಡೆ (ಎಡಭಾಗ ಮತ್ತು ಬಲಭಾಗ) ಸಮವಾಗುವುದೋ, ಆ ಅವ್ಯಕ್ತ ಪದದ ಬೆಲೆಯನ್ನು ಕಂಡು ಹಿಡಿಯುವುದನ್ನು ‘ಸಮೀಕರಣದ ಪರಿಹಾರ (’‘solution’ )ಕಂಡು ಹಿಡಿಯುವುದು ಎನ್ನುತ್ತೇವೆ. ಇದನ್ನೇ ‘ಸಮೀಕರಣ ಬಿಡಿಸುವುದು’ ಎಂತಲೂ ಕರೆಯುತ್ತೇವೆ.
ಮೇಲಿನ ಉದಾಹರಣೆಯಲ್ಲಿ x =2 - ಇದು ಸಮೀಕರಣದ ಪರಿಹಾರ.ಈ ಮೇಲಿನ ಸಮೀಕರಣಕ್ಕೆ x=1 ಪರಿಹಾರವಲ್ಲ.ಏಕೆಂದರೆ 1ನ್ನು x ಸ್ಥಾನದಲ್ಲಿ ಆದೇಶಿಸಿದಾಗ LHS
= 10 ,RHS=13 ಆಗುತ್ತದೆ. ಹೀಗಾಗಿ LHS ![]()
2.7 ಸಮಸ್ಯೆ
1 : ಈ ಸಮೀಕರಣ ಬಿಡಿಸಿ (x ನ ಬೆಲೆ ಕಂಡು ಹಿಡಿ):
5*(2x-3) = 2*(3x-7)
ಪರಿಹಾರ:
|
ಹಂತ |
ಹೇಳಿಕೆ |
ವಿವರಣೆ |
|
1 |
5*(2x-3) =
2*(3x-7) |
ಪರಿಹಾರ |
|
2 |
10x -15 = 6x -14 |
ದತ್ತ ಸಮೀಕರಣ |
|
3 |
10x -6x= -14+15 |
ಸುಲಭರೂಪಕ್ಕೆ ತಂದಿದೆ. |
|
4 |
4x = 1:i,e x = 1/4 |
6x ಮತ್ತು 15 ಇವುಗಳನ್ನು ಚಿಹ್ನೆ ಬದಲಾಯಿಸಿ ಇನ್ನೊಂದು ಬದಿಗೆ ವರ್ಗಾಯಿಸಿದೆ. |
ತಾಳೆ:
1/4 ನ್ನ x ದತ್ತ ಸಮೀಕರಣದಲ್ಲಿ ಆದೇಶಿಸಿ.
ಎಡಭಾಗ= 5*(2*1/4 -3) =
5*(1/2-3) = 5*(-5/2) = -25/2
ಬಲಭಾಗ= 2*(3*1/4-7) = 2*(3/4-7) = 2*(-25/4) = -25/2
ಎಡಭಾಗ= ಬಲಭಾಗ= -25/2, x =1/4 ಇದು ಸರಿಯಾದ ಪರಿಹಾರ.
2.7 ಸಮಸ್ಯೆ
2 : x ನ ಬೆಲೆ ಕಂಡುಹಿಡಿ .
![]() = 1/2
= 1/2
ಪರಿಹಾರ:
ಸಮೀಕರಣದ ಎರಡೂ ಬದಿಗಳನ್ನು ವರ್ಗಮಾಡಿ.
(x-2)/(x+1) = 1/4
ಅಡ್ಡ ಗುಣಕಾರ ಮಾಡಿ.
4(x-2) =
x+1
i.e. 4x – 8 = x+1 (ಸುಲಭರೂಪಕ್ಕೆ ತಂದಿದೆ.)
i.e. 4x
–x = 1+8 ( ವರ್ಗಾಯಿಸಿದೆ.)
i.e. 3x = 9
![]() x=3
x=3
ತಾಳೆ:
xನ ಬೆಲೆ 3ನ್ನ ದತ್ತ ಸಮೀಕರಣದಲ್ಲಿ ಆದೇಶಿಸಿ.![]() = 1/2
= 1/2
2.7 ಸಮಸ್ಯೆ
3: ಮೂರು ಅನುಕ್ರಮ ಸಮ ಸಂಖ್ಯೆಗಳ ಮೊತ್ತ 252. ಆದರೆ ಆ ಸಂಖ್ಯೆಗಳಾವುವು?
ಪರಿಹಾರ:
ಹಂತ 1 : ಮೊದಲ ಸಮ ಸಂಖ್ಯೆ x ಆಗಿರಲಿ
ಹಂತ 2 : ಮುಂದಿನ ಅನುಕ್ರಮ ಸಮ ಸಂಖ್ಯೆಗಳು = (x+2) ಮತ್ತು (x+4).
ಹಂತ 3 :
x+(x+2)+(x+4) = 3x+6 = 252. (ದತ್ತ)
![]() 3x+6 = 252
3x+6 = 252
3x =
252-6=246
x = 82
ಮೂರು
ಅನುಕ್ರಮ ಸಮ ಸಂಖ್ಯೆಗಳು 82(=x),
84(=x+2)
86(=x+4)
ತಾಳೆ:
82,
84, 86 ಈ ಮೂರು ಅನುಕ್ರಮ ಸಮಸಂಖ್ಯೆಗಳನ್ನು ಕೂಡಿಸಿ. ಮೊತ್ತ = 252
2.7 ಸಮಸ್ಯೆ 4: ಒಂದು ಹಡಗು ಪ್ರವಾಹದ ದಿಕ್ಕಿನಲ್ಲಿ ಒಂದು ಬಂದರಿನಿಂದ ಇನ್ನೊಂದು ಬಂದರಿಗೆ 9 ಗಂಟೆಗಳಲ್ಲಿ ತಲಪುವುದು. ಪ್ರವಾಹದ ವಿರುದ್ಧ ದಿಕ್ಕಿನಲ್ಲಿ ಅದೇ ದೂರವನ್ನು ಪ್ರಯಾಣ ಮಾಡಲು 10 ಗಂಟೆಗಳನ್ನು ತೆಗೆದುಕೊಳ್ಳುವುದು. ಪ್ರವಾಹದ ವೇಗ ಗಂಟೆಗೆ 1ಕಿ.ಮಿ. ಇದ್ದರೆ, ಎರಡು ಬಂದರುಗಳಿಗಿರುವ ದೂರವನ್ನು ಕಂಡು ಹಿಡಿಯಿರಿ.
ಪರಿಹಾರ:
|
1) ನಿಶ್ಚಲ ನೀರಿನಲ್ಲಿ ಹಡಗಿನ ವೇಗ ಗಂಟೆಗೆ x ಕಿ.ಮೀ. ಆಗಿರಲಿ. ಪ್ರವಾಹದ
ದಿಕ್ಕಿನಲ್ಲಿ ಹಡಗಿನ ವೇಗ = (x+1) ಕಿ.ಮೀ./ಗಂ. ಪ್ರವಾಹದ
ವಿರುದ್ಧವಾಗಿ ಹಡಗಿನ ವೇಗ = (x-1) ಕಿ.ಮೀ./ಗಂ. ಪ್ರವಾಹದ ನೇರದಲ್ಲಿ 9
ಗಂಟೆಯಲ್ಲಿ ಚಲಿಸಿದ ದೂರ =9(x+1). ಪ್ರವಾಹದ
ವಿರುದ್ಧವಾಗಿ 10 ಗಂಟೆಯಲ್ಲಿ ಚಲಿಸಿದ ದೂರ = 10(x-1) 2) ಈ ಎರಡೂ ದೂರಗಳು ಪರಸ್ಪರ ಸಮ
3) 9x+9
=10x-10 :9+10 =10x-9x(ವರ್ಗಾಯಿಸಿದೆ.) |
|
ತಾಳೆ:
ಪ್ರವಾಹದ ದಿಕ್ಕಿನಲ್ಲಿ ಹಡಗಿನ ವೇಗ= (ದೂರ/ಸಮಯ)- ಪ್ರವಾಹದ ವೇಗ= (180/9)-1 = (20-1) ಕಿ.ಮೀ./ಗಂ=19 ಕಿ.ಮೀ./ಗಂ
ಪ್ರವಾಹದ ವಿರುದ್ಧದಲ್ಲಿ ಹಡಗಿನ ವೇಗ= (ದೂರ/ಸಮಯ)+ ಪ್ರವಾಹದ ವೇಗ= (180/10) +1 = (18+1) ಕಿ.ಮೀ./ಗಂ=19 ಕಿ.ಮೀ./ಗಂ
ಈ
ಮೇಲಿನಿಂದ ನಮ್ಮ ಪರಿಹಾರ ಸರಿಯಾಗಿದೆ ಎಂದು ತಿಳಿಯಬಹುದು.
2.7 ಸಮಸ್ಯೆ
5: ಒಂದು ಸಂಖ್ಯೆಯಲ್ಲಿ ಎರಡು ಅಂಕಿಗಳಿವೆ. ದಶಕಸ್ಥಾನದ ಅಂಕೆಯು ಏಕಸ್ಥಾನದ ಅಂಕದ
ಎರಡರಷ್ಟಿದೆ. ಸಂಖ್ಯೆಯ ಅಂಕಗಳನ್ನು ಅದಲು ಬದಲು ಮಾಡಿದಾಗ ಬರುವ ಸಂಖ್ಯೆಯು ಮೂಲ ಸಂಖ್ಯೆಗಿಂತ 27 ಕಡಿಮೆ ಇದ್ದರೆ ಮೂಲ ಸಂಖ್ಯೆಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಪರಿಹಾರ:
|
1 ಸಂಖ್ಯೆಯ ಏಕ ಸ್ಥಾನದ ಅಂಕೆ x ಆಗಿರಲಿ. ದಶಕಸ್ಥಾನದ ಅಂಕೆಯು ಏಕಸ್ಥಾನದ ಅಂಕೆಯ 2 ರಷ್ಟಿರುವುದರಿಂದ, ದಶಕ ಸ್ಥಾನದ ಅಂಕೆ =2x. ಸಂಖ್ಯೆಯಲ್ಲಿ 2 ಅಂಕಿಗಳಿರುವುದರಿಂದ ಅದರ ಬೆಲೆ =10*ದಶಕ ಸ್ಥಾನದ ಅಂಕೆ+ ಏಕ ಸ್ಥಾನದ ಅಂಕೆ = 10*2x+x. =20x+x = 21 x -------------è (1) ಅಂಕಿಗಳನ್ನು ಅದಲು ಬದಲು ಮಾಡಿದಾಗ, ದಶಕ ಸ್ಥಾನದಲ್ಲಿ x ಬರುತ್ತದೆ, 2x ಏಕಸ್ಥಾನದಲ್ಲಿ ಬರುತ್ತದೆ. ಆಗ ಸಂಖ್ಯೆಯ ಬೆಲೆ = 10* ದಶಕ ಸ್ಥಾನದ ಅಂಕೆ + ಏಕಸ್ಥಾನದ ಅಂಕೆ. = 10*x+2x =10x+2x
= 12 x --------------è ತಿರುಗಿಸಿದ ಸಂಖ್ಯೆ. ದತ್ತಾಂಶದಂತೆ, ಹೊಸ ತಿರುಗಿಸಿದ ಸಂಖ್ಯೆ = ಹಳೇ
ಸಂಖ್ಯೆ – 27
27 =9x |
|
ತಾಳೆ:
ಮೂಲ ಸಂಖ್ಯೆ = 63
ಅಂಕೆಗಳನ್ನು ಅದಲು
ಬದಲು ಮಾಡಿದಾಗ ಬರುವ ಸಂಖ್ಯೆ = 36(36 = 63
-27.)
ಇದು ದತ್ತಾಂಶಕ್ಕೆ
ಸರಿಯಾಗಿದೆ.
2.7 ಸಮಸ್ಯೆ 6: ಒಂದು ಆಯತದ ಉದ್ದವು
ಅಗಲಕ್ಕಿಂತ 4 ಸೆಂ.ಮೀ ಹೆಚ್ಚಿದೆ. ಸುತ್ತಳತೆಯು ಅಗಲಕ್ಕಿಂತ 11ಸೆಂ.ಮೀ. ಹೆಚ್ಚಿದ್ದಲ್ಲಿ ಆಯತದ ಉದ್ದ ಮತ್ತು ಅಗಲಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಪರಿಹಾರ:
ಹಂತ 1: ಆಯತದ ಅಗಲ x ಆಗಿರಲಿ. ಉದ್ದ = x+4.
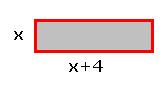
ಆಯತದ ಸುತ್ತಳತೆ P = 2* ಉದ್ದ + 2* ಅಗಲ
= 2(x+4)+2x
= 2x+8+2x
P = 4x +8 --------------è (1)
ಆದರೆ ದತ್ತಾಂಶದಂತೆ, ಸುತ್ತಳತೆಯು ಅಗಲಕ್ಕಿಂತ 11ಸೆಂ.ಮೀ ಹೆಚ್ಚಿದೆ.
P = x+11
--------------è (2)
ಹಂತ 2 :
ಸಮೀಕರಣ (1) ಮತ್ತು (2) ರಿಂದ,
2x+8+2x = x+11
4x+8 = x+11
4x-x = 11-8(x ಮತ್ತು 8ರ ಸ್ಥಾನ ಬದಲಿಸಿದೆ.)
3x = 3
![]() x = 1.
x = 1.
ಆಯತದ ಅಗಲ =11ಸೆಂ.ಮೀ., ಉದ್ದ =
x+4 = 5 ಸೆಂ.ಮೀ.
ತಾಳೆ:
ಆಯತದ ಸುತ್ತಳತೆ P = 2* ಉದ್ದ + 2* ಅಗಲ
= 2*5+2*1
= 10+2
= 12 ಸೆಂ.ಮೀ
= 11 ಸೆಂ.ಮೀ +1 ಸೆಂ.ಮೀ
= 11 ಸೆಂ.ಮೀ + ಅಗಲ
2.7 ಸಮಸ್ಯೆ 7: ಒಂದು ಭಿನ್ನರಾಶಿಯಲ್ಲಿ ಅಂಶದ ಎರಡರಷ್ಟು ಛೇದಕ್ಕಿಂತ 2 ಹೆಚ್ಚಿದೆ.3ನ್ನ ಅಂಕ ಮತ್ತು ಛೇದ ಎರಡಕ್ಕೂ ಸೇರಿಸಿದಾಗ ಬರುವ ಭಿನ್ನರಾಶಿಯು 2/3 ಆದರೆ, ಮೂಲ ಭಿನ್ನರಾಶಿಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಪರಿಹಾರ:
ಹಂತ
1: ಭಿನ್ನರಾಶಿಯ ಅಂಶವು
x
ಆಗಿರಲಿ.
ಅಂಶದ ಎರಡರಷ್ಟು = ಛೇದಕ್ಕಿಂತ 2 ಹೆಚ್ಚು.
2x = ಛೇದ +2.
ಛೇದ= 2x-2
ಮೂಲ ಭಿನ್ನರಾಶಿ = x/2x-2
3 ನ್ನ ಛೇದಕ್ಕೆ ಕೂಡಿಸಿದಾಗ , ಹೊಸ ಛೇದ = (2x-2) +3=2x+1
3 ನ್ನ ಅಂಶಕ್ಕೆ ಕೂಡಿಸಿದಾಗ ಹೊಸ ಅಂಶ = x+3
ಹೊಸ ಭಿನ್ನರಾಶಿ = (x+3)/ (2x+1)
ದತ್ತಾಂಶದಂತೆ ಹೊಸ
ಭಿನ್ನರಾಶಿ 2/3
ಹಂತ 2 : 2/3
= (x+3)/(2x+1)
--------------è(1)
ಅಡ್ಡ ಗುಣಕಾರ ಮಾಡಿದಾಗ,
2*(2x+1) =3
(x+3) --------------è(2)
4x+2 =3x+9 (3x ಮತ್ತು 2 ನ್ನ ಪರಸ್ಪರ ವರ್ಗಾಯಿಸಿದೆ.)
4x-3x= 9-2
x= 7
![]() ಮೂಲ ಭಿನ್ನರಾಶಿಯ ಛೇದ = 2x-2
=14-2=12
ಮೂಲ ಭಿನ್ನರಾಶಿಯ ಛೇದ = 2x-2
=14-2=12
ಮೂಲ ಭಿನ್ನರಾಶಿ = 7/12
ತಾಳೆ:
ಮೂಲ ಭಿನ್ನರಾಶಿ = 7/12
3ನ್ನ ಅಂಕ ಮತ್ತು ಛೇದಗಳಿಗೆ ಕೂಡಿಸಿದಾಗ = 10/15 =
2/3 -
ದತ್ತ
2.7 ಸಮಸ್ಯೆ 8: ದೊಡ್ಡಭಾಗವನ್ನು
ಚಿಕ್ಕಭಾಗದಿಂದ ಭಾಗಿಸಿದಾಗ, ಭಾಗಲಬ್ಧ 2 ಮತ್ತು ಶೇಷ 5 ಆಗಿರುವಂತೆ, 32 ನ್ನ ಎರಡು ಭಾಗ ಮಾಡಿ..
ಪರಿಹಾರ:
|
ದೊಡ್ಡಭಾಗ = ಆಗಿರಲಿ
ಚಿಕ್ಕಭಾಗ = 32-x ಭಾಜ್ಯ= ಭಾಗಲಬ್ಧ*ಭಾಜಕ ± ಶೇಷ.. x/(32-x) = 2+ 5(±ಶೇಷ.) ಅಭ್ಯಾಸ: ಈ ಸಮೀಕರಣವನ್ನು ಬಿಡಿಸಿ(x =23 ,ಇನ್ನೊಂದು ಸಂಖ್ಯೆ = 9) |
|
2.7 ಸಮಸ್ಯೆ 9: x2-9/( x2+5)
= -5/9
ಆಗಿರುವ ಸಮೀಕರಣದಲ್ಲಿ x ನ
ಧನಾತ್ಮಕ ಬೆಲೆಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಪರಿಹಾರ:
ದತ್ತಾಂಶದಂತೆ x2-9/( x2+5) = -5/9
ಅಡ್ಡ ಗುಣಾಕಾರ ಮಾಡಿದಾಗ 9(x2-9) = -5(x2+5)
ಸಂಕ್ಷೇಪಿಸಿದಾಗ 9x2-81 = -5x2 -25
ಸ್ಥಾನ ಬದಲಾಯಿಸಿದಾಗ 14x2 = 56
![]() x2
= 4
x2
= 4
![]() x = +2 ಅಥವಾ -2
x = +2 ಅಥವಾ -2
ತಾಳೆ:
ದತ್ತ ಸಮೀಕರಣದಲ್ಲಿ x=2 ನ್ನು ಆದೇಶಿಸಿದಾಗ, LHS = -5/9 = RHS, ಆದ್ದರಿಂದ ಇದು ಸರಿಯಾದ ಪರಿಹಾರ.
2.7 ಸಮಸ್ಯೆ 10: ದುಂಬಿಗಳ ಸಮೂಹದಲ್ಲಿ 1/5 ರ ಭಾಗ ಕದಂಬ ವೃಕ್ಷಕ್ಕೂ, 1/3 ನೇ ಭಾಗ ಶಿಲೀಂಧ್ರಕ್ಕೂ ಹೊರಟವು. ಅವೆರಡರ ವ್ಯತ್ಯಾಸದ ಮೂರರಷ್ಟು ಕುಟಜ ವೃಕ್ಷಕ್ಕೂ ಹೋದ ಮೇಲೆ ಉಳಿದ ಒಂದೇ ಒಂದು ದುಂಬಿಯು ಕೇತಕಮಾಲತೀ ಪುಷ್ಪದ ಸುಗಂಧದಿಂದ ಆಕರ್ಷಿಸಲ್ಪಟ್ಟು ಆಕಾಶದಲ್ಲಿ ಹಾರಾಡುತ್ತಿತ್ತು. ಹಾಗಾದರೆ ಎಲೈ ಲೀಲಾವತಿ, ದುಂಬಿಗಳ ಒಟ್ಟು ಸಂಖ್ಯೆಎಷ್ಟು? (ಲೀಲಾವತಿ ಶ್ಲೋಕ 56)
ಪರಿಹಾರ:
ಒಟ್ಟು ಸಂಖ್ಯೆ x ಇರಲಿ.
|
ಹಂತ |
ಎಲ್ಲಿಗೆ |
ಎಷ್ಟು |
|
1 |
ಕದಂಬಕ್ಕೆ |
(x/5) |
|
2 |
ಶಿಲೀಂಧ್ರಕ್ಕೆ |
(x/3) |
|
3 |
ಮೇಲಿನವುಗಳ
ವ್ಯತ್ಯಾಸ |
(x/3) – (x/5) =
(2x/15) |
|
4 |
ಕುಟಜಕ್ಕೆ |
3*(2x/15)=(2x/15) |
|
5 |
ಉಳಿದದ್ದು |
1 |
![]() x- {(x/5)+(x/3)+(2x/5) =1
x- {(x/5)+(x/3)+(2x/5) =1
![]() {15x-(3x+5x+6x)/15} =1
{15x-(3x+5x+6x)/15} =1
![]() x=15
x=15
ತಾಳೆ:
ಕದಂಬಕ್ಕೆ 3, ಶಿಲೀಂಧ್ರಕ್ಕೆ 5, ಕುಟಜಕ್ಕೆ 6 { =3*(5-3)} ಉಳಿದದ್ದು 1
2.7 ಸಮಸ್ಯೆ 11: ಒಬ್ಬ ಯಾತ್ರಿಕನು ತನ್ನ ಹಣದ ಅರ್ಧ ಭಾಗವನ್ನು ಪ್ರಯಾಗದಲ್ಲಿಯೂ, ಉಳಿದುದರ 2/9 ಭಾಗವನ್ನು ಕಾಶಿಯಲ್ಲಿಯೂ, ಉಳಿದುದರ 1/4 ಭಾಗವನ್ನು ತೆರಿಗೆಗಳಿಗೂ, ಇನ್ನುಳಿದುದರ 6/10 ಭಾಗವನ್ನು ಗಯೆಯಲ್ಲಿಯೂ ಖರ್ಚುಮಾಡಿದ ನಂತರ ಉಳಿದ 63 ನಿಷ್ಕಗಳನ್ನು(ಹಣದ ಅಳತೆ) ಮನೆಗೆ ತಂದರೆ, ಯಾತ್ರೆಗೆ ತೆಗೆದು ಕೊಂಡು ಹೋದ ಹಣ ಎಷ್ಟು?(ಲೀಲಾವತಿ ಶ್ಲೋಕ 55)
ಪರಿಹಾರ:
ಒಟ್ಟು ಸಂಖ್ಯೆ x ಇರಲಿ.
|
ಹಂತ |
ಎಲ್ಲಿ/ಏತಕ್ಕೆ |
ಎಷ್ಟು |
ನಂತರ ಉಳಿದದ್ದು |
|
1 |
ಪ್ರಯಾಗ |
(x/2) |
x-(x/2) = (x/2) |
|
2 |
ಕಾಶಿ |
(2/9)*(x/2)=(x/9) |
(x/2)-(x/9) = (7x/18) |
|
3 |
ತೆರಿಗೆ |
(1/4)*(7x/18) =(7x/72) |
(7x/18) - (7x/72)= (21x/72) =(7x/24) |
|
4 |
ಗಯೆ |
(6/10)*(7x/24)=(7x/40) |
(7x/24)- (7x/40) ={(35x-21x)/120}=(7x/60) |
|
5 |
ಉಳಿದದ್ದು |
63 |
|
![]() (7x/60)
=63
(7x/60)
=63
![]() x=540
x=540
ತಾಳೆ:
ನೀವೇ
ಮಾಡಿ
2.7 ಕಲಿತ ಸಾರಾಂಶ
|
ಸಂ |
ಕಲಿತ ಮುಖ್ಯಾಂಶಗಳು |
|
1 |
ಪದಗಳನ್ನು ಸಮೀಕರಣದ ಆಚೀಚೆಗೆ ಚಿಹ್ನೆ ಬದಲಾಯಿಸಿ
ವರ್ಗಾಯಿಸುವುದು |
|
2 |
ಎಡಭಾಗ ಮತ್ತು ಬಲಭಾಗವನ್ನು ಸಂಕ್ಷೇಪಿಸಿ, ಅವ್ಯಕ್ತ ಪದಗಳು ಒಂದು ಬದಿಗೆ, ಸ್ಥಿರಾಂಕಗಳು ಮತ್ತೊಂದು ಬದಿಗೆ ಬರುವಂತೆ ಮಾಡಿ, ಸಮೀಕರಣದ ಪರಿಹಾರ ಕಂಡುಹಿಡಿಯುವುದು. |