4.5 ಸರಳ ಬಡ್ಡಿ (Simple Interest):

ಬಾಸ್ಕರರು ತಮ್ಮ ಲೀಲಾವತೀ ಪುಸ್ತಕದಲ್ಲಿ ಬಡ್ಡಿ ಲೆಕ್ಕಾಚಾರ ಮಾಡಿರುವುದು ನಿಮಗೆ ಆಶ್ಚರ್ಯ ಉಂಟು ಮಾಡುವುದೇ?( ಸಮಸ್ಯೆ 4.5.4 ನೋಡಿ)

ಕೆಳಗಿನ ಸಮಸ್ಯೆ ಆಸಕ್ತಿ ತರಿಸುವುದೇ?

ಮೂರು ಜನ ಅಕ್ಕ ತಂಗಿಯರ ವಯಸ್ಸು 5, 10 ಮತ್ತು15 ವರ್ಷಗಳು ಆಗಿರುವಾಗ ಅವರ ತಂದೆ ಬ್ಯಾಂಕ್ ನಲ್ಲಿ 5% ಸರಳ ಬಡ್ಡಿಯಲ್ಲಿ 80,250 ರೂಪಾಯಿಗಳನ್ನು ಇರಿಸಿದರು. ಮಕ್ಕಳಿಗೆ 20 ವರ್ಷಗಳಾದಾಗ, ಅವರಲ್ಲಿ ಪ್ರತಿಯೊಬ್ಬರಿಗೂ ಸಮ ಪಾಲು ಸಿಗುವಂತಾಗಬೇಕಾದರೆ, ತಂದೆ ಬ್ಯಾಂಕ್ ನಲ್ಲಿ ಇರಿಸಿದ ಹಣದಲ್ಲಿ ಪ್ರತಿ ಮಕ್ಕಳ ಪಾಲು ಎಷ್ಟು?

ಬ್ಯಾಂಕಿನಲ್ಲಿ ನಾವಿಟ್ಟ ಹಣ ಅಥವಾ ಬ್ಯಾಂಕು ಸಾಲಗಾರರಿಗೆ ಕೊಟ್ಟ ಹಣ – ಇದನ್ನು ‘ಅಸಲು ಹಣ’ (Principal) ಎನ್ನುತ್ತೇವೆ. ಬ್ಯಾಂಕಿನಲ್ಲಿ ನಾವು ಎಷ್ಟು ಸಮಯದವರೆಗೆ ಹಣವನ್ನು ಇಡುತ್ತೇವೆ ಅಥವಾ ಎಷ್ಟು ಸಮಯದವರೆಗೆ ಸಾಲಗಾರ ಸಾಲ ಪಡೆದುಕೊಂಡಿದ್ದಾನೆ, ಅದನ್ನು “ಕಾಲ ಅಥವಾ ಅವಧಿ” (Period or Term) ಎನ್ನುತ್ತೇವೆ. ಬ್ಯಾಂಕಿನವರು ನಮ್ಮ ಹಣಕ್ಕೆ ಕೊಡುವ ಬಡ್ಡಿ ಅಥವಾ ಬ್ಯಾಂಕ್ ಸಾಲಗಾರನಿಂದ ವಸೂಲಿ ಮಾಡುವ ಬಡ್ಡಿಯನ್ನು ವರ್ಷಕ್ಕೆ ಶೇಕಡಾದರ (%)ದಲ್ಲಿ ಲೆಕ್ಕಹಾಕುತ್ತಾರೆ. ಈ ಹಿಂದೆಯೇ ತಿಳಿಸಿದಂತೆ ಬ್ಯಾಂಕಿಗೆ ಅದರದ್ದೇ ಆದ ಖರ್ಚುಗಳಿವೆ. (ನೌಕರರ ಸಂಬಳ, ಕಟ್ಟಡದ ಬಾಡಿಗೆ, ವಿದ್ಯುತ್ ಬಿಲ್, ಇತ್ಯಾದಿ). ಅಲ್ಲದೆ ಬ್ಯಾಂಕು ನಾವಿಟ್ಟ ಹಣಕ್ಕೂ ಬಡ್ಡಿ ಕೊಡುತ್ತದೆ. ಸಾಲಗಳ ಮೇಲೆ ಬರುವ ಬಡ್ಡಿ ಬ್ಯಾಂಕಿಗೆ ಬರುವ ಆದಾಯದ ಮುಖ್ಯ ಮೂಲ. ಆದ್ದರಿಂದ ಬ್ಯಾಂಕು ಲಾಭದಲ್ಲಿದ್ದು ಮುಂದುವರಿಯಲೋಸುಗ, ಅದು ನಮಗೆ ಕೊಡುವ ಬಡ್ಡಿಗಿಂತಲೂ ಸಾಲಗಾರರಿಂದ ಹೆಚ್ಚು ಬಡ್ಡಿ ವಸೂಲು(ಸುಮಾರು 5% ಹೆಚ್ಚು) ಮಾಡುತ್ತದೆ.

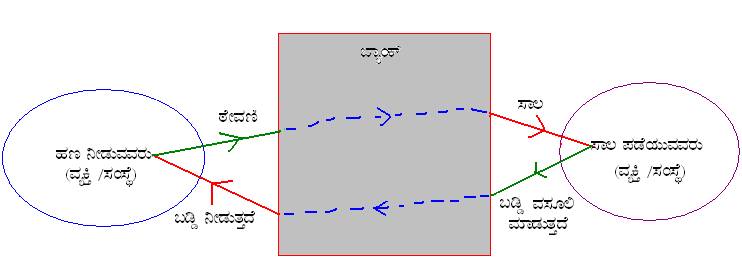
ಈ ಕೆಳಗಿನ ಹೇಳಿಕೆಗಳನ್ನ ಗಮನಿಸುವಾ:-

4.5 ಉದಾ 1: ರಾಮನು 5000ರೂ.ಗಳನ್ನು ‘ಸ್ಟೇಟ್ ಬ್ಯಾಂಕ್ ಆಫ್ ಇಂಡಿಯಾ’ದಲ್ಲಿ 8% ಬಡ್ಡಿದರದಲ್ಲಿ 6 ವರ್ಷಗಳಿಗೆ ಠೇವಣಿ ಇರಿಸಿದ್ದಾನೆ. (ಇದರ ಅರ್ಥ ಬ್ಯಾಂಕು 6 ವರ್ಷಗಳವರೆಗೆ ಹಣ ತನ್ನಲ್ಲಿರುವಂತೆ ರಾಮನಿಂದ 5000 ರೂಪಾಯಿಗಳನ್ನು ಆರಂಭಿಕ ಠೇವಣಿಯಾಗಿ ಪಡೆದಿದೆ. ಬ್ಯಾಂಕಿಗೆ ಹಣವನ್ನು ಕೊಟ್ಟದ್ದಕ್ಕಾಗಿ ರಾಮನಿಗೆ 6 ವರ್ಷಗಳಷ್ಟು ದೀರ್ಘ ಅವಧಿಯವರೆಗೆ ವರ್ಷಕ್ಕೆ 8% ರ ದರದಲ್ಲಿ ಬಡ್ಡಿಯನ್ನು ಕೊಡುತ್ತದೆ.) ಹಾಗಾದರೆ ರಾಮನಿಗೆ ಒಂದು ವರ್ಷದಲ್ಲಿ ಸಿಗುವ ಬಡ್ಡಿ ಎಷ್ಟು? 6 ವರ್ಷಗಳಲ್ಲಿ ಸಿಗುವ ಒಟ್ಟು ಬಡ್ಡಿ ಎಷ್ಟು?

ರಾಮನಿಗೆ 8% ಬಡ್ಡಿ ಎಂಬುದರ ಅರ್ಥವೇನು?(ಬ್ಯಾಂಕು ರಾಮನಿಗೆ ಪ್ರತೀ ವರ್ಷ ಪ್ರತೀ 100ರೂ.ಗಳಿಗೆ 8 ರೂ. ಬಡ್ಡಿಯನ್ನು ಕೊಡುತ್ತದೆ)

ರಾಮನು 100 ರೂ.ಗಳಿಗೆ 8 ರೂಪಾಯಿ ಬಡ್ಡಿ ಪಡೆಯುತ್ತಾನೆ. (8% ಬಡ್ಡಿ)

5000 ರೂ.ಗಳಿಗೆ ಬಡ್ಡಿ = 8*5000/100 = 400ರೂ (ಒಂದು ವರ್ಷಕ್ಕೆ)

ರಾಮನು 5000ರೂ.ಗಳನ್ನು ಠೇವಣಿ ಇರಿಸಿದ್ದರಿಂದ 6 ವರ್ಷಗಳವರೆಗೆ ಪ್ರತೀ ವರ್ಷ 400ರೂ. ಪಡೆಯುತ್ತಾನೆ.

ಒಟ್ಟು 6 ವರ್ಷಗಳಲ್ಲಿ ಅವನು ಬ್ಯಾಂಕಿನಿಂದ ಪಡೆಯುವ ಬಡ್ಡಿ = 400*6= ರೂ.2400

ಅಲ್ಲದೆ, 6 ವರ್ಷಗಳ ನಂತರ ಅವನು ಅಸಲು ಹಣ 5000ರೂ.ಗಳನ್ನು ಹಿಂದೆ ಪಡೆಯುತ್ತಾನೆ.

ಬ್ಯಾಂಕಿನ ವ್ಯವಹಾರದಲ್ಲಿ ಹೇಳುವುದಾದರೆ, ಈ ರೀತಿಯ ಬಡ್ಡಿ ಲೆಕ್ಕಾಚಾರವನ್ನು “ಸರಳ ಬಡ್ಡಿ” (Simple Interest) ಎನ್ನುತ್ತೇವೆ.

P = ಅಸಲು ಹಣ (ಠೇವಣಿ ಇರಿಸಿದ ಅಥವಾ ಪಡೆದ ಹಣ)

N = ಠೇವಣಿಯ/ಸಾಲದ ಅವಧಿ(ಸಾಮಾನ್ಯವಾಗಿ ವರ್ಷಗಳಲ್ಲಿ)

R = ಬಡ್ಡಿಯದರ (100 ರೂ.ಗಳಿಗೆ 1 ವರ್ಷಕ್ಕೆ ಸಿಗುವ ಬಡ್ಡಿ)

I = ಸಾಲಗಾರನು ಬ್ಯಾಂಕಿಗೆ ಕೊಡುವ(ಅಥವಾ ಬ್ಯಾಂಕು ಠೇವಣಿದಾರನಿಗೆ) ಕೊಡುವ ಬಡ್ಡಿ ಹಣ.

A = ಬ್ಯಾಂಕು ಅವಧಿ ಮುಗಿದಾಗ ಠೇವಣಿದಾರನಿಗೆ ಕೊಡುವ(ಅಥವಾ ಸಾಲಗಾರನು ಬ್ಯಾಂಕಿಗೆ ಕೊಡುವ) ಒಟ್ಟು ಹಣ.(A = P+I )

ಸರಳ ಬಡ್ಡಿಯ ಲೆಕ್ಕಾಚಾರಕ್ಕೆ ನಾವು ಈ ಸೂತ್ರವನ್ನು ಉಪಯೋಗಿಸುತ್ತೇವೆ:

ಸರಳ ಬಡ್ಡಿ (SI)= (P*N*R)/100

ನಾವೀಗ ಮೇಲಿನ ಉದಾಹರಣೆಯಲ್ಲಿನ ಬಡ್ಡಿ ಲೆಕ್ಕಾಚಾರವನ್ನ ಸೂತ್ರ ಉಪಯೋಗಿಸಿ ಮಾಡುವಾ.

ತಾಳೆ:

P = 5000

N= 6 ವರ್ಷ

R = 8%

ಈ ಬೆಲೆಗಳನ್ನು I= (P*N*R)/100 ಸೂತ್ರದಲ್ಲಿ ಆದೇಶಿಸಿದಾಗ,

I = (5000*6*8)/100 = 50*6*008 =2400

ಈ ಉತ್ತರ ನಾವು ಮೇಲೆಯೇ ಪಡೆದಿದ್ದೇವೆ

A = P+I ಮತ್ತು I = P*N*R/100

A = P+ (P*N*R)/100 = P {1+ (N*R)/100}

ಈಗ ನಾವು ಸಾಲಗಾರನ ಉದಾಹರಣೆ ನೋಡುವಾ.

4.5 ಸಮಸ್ಯೆ 1: ಶ್ರೀಯುತ ರಾಜ್ ರವರು ಭಾರತೀಯ ಸ್ಟೇಟ್ ಬ್ಯಾಂಕಿನಿಂದ 12% ಬಡ್ಡಿಯ ದರದಲ್ಲಿ 7 ವರ್ಷಗಳ ಅವಧಿಗೆ ರೂ.1,50,000 ಸಾಲ ಪಡೆದರು. ಹಾಗಾದರೆ 7 ವರ್ಷಗಳಿಗೆ ಅವರು ಕೊಡಬೇಕಾದ ಒಟ್ಟು ಬಡ್ಡಿ ಎಷ್ಟು? ಹಾಗೆಯೇ 7 ವರ್ಷಗಳ ನಂತರ ಅವರು ವಾಪಾಸು ಕೊಡಬೇಕಾದ ಒಟ್ಟು ಹಣ ಎಷ್ಟು? (ಅವರು ಅಸಲು ಹಣದ ಜತೆಗೇ ಒಟ್ಟು ಬಡ್ಡಿಯ ಹಣವನ್ನು ಕೊಡುತ್ತಾರೆಂದು ಭಾವಿಸಿ.)

ಪರಿಹಾರ:

ಈ ಸಮಸ್ಯೆಯಲ್ಲಿ

P = 150000

R= 12%

N =7

ಈ ಬೆಲೆಗಳನ್ನು ಸಮೀಕರಣದಲ್ಲಿ ಆದೇಶಿಸಿದಾಗ,

ಒಟ್ಟು ಬಡ್ಡಿ = 150000*7*(12/100) = 1500*7*12 = 126000

ಅಸಲು ಹಣ ಮತ್ತು ಬಡ್ಡಿಯನ್ನು ಒಟ್ಟಿಗೇ ಕೊನೆಯಲ್ಲಿ ಕಟ್ಟುವುದರಿಂದ,

ಅವರು ಕಟ್ಟಬೇಕಾದ ಒಟ್ಟು ಹಣ =1,50,000(ಅಸಲು)+1,26,000 (ಬಡ್ಡಿ)

= 2,76,000 ರೂ

4.5 ಸಮಸ್ಯೆ 2: ಒಂದು ಮೊಬಲಗು 14% ಸರಳಬಡ್ಡಿ ದರದಲ್ಲಿ 3 ವರ್ಷಗಳಲ್ಲಿ 3,360 ರೂ. ಮೊತ್ತವಾಗುತ್ತದೆ. ಹಾಗಾದರೆ, ಅದೇ ಮೊಬಲಗು 6% ದರದಲ್ಲಿ 3 ½ ತಿಂಗಳುಗಳಲ್ಲಿ ಗಳಿಸುವ ಬಡ್ಡಿಯನ್ನು ಕಂಡು ಹಿಡಿಯಿರಿ.

ಪರಿಹಾರ:

ಇಲ್ಲಿ,

A = 3360, R =14 N=3

ಆದರೆ, A = P{1+ (N*R)/100}

3360 = P{1+ (3*14)/100} = p*142/100

P = 3360*100/142 = 2366

ಈಗ, R = 6 N = 3 1/2 ತಿಂಗಳು = (3.5/12) ವರ್ಷಗಳು

ಸರಳ ಬಡ್ಡಿ SI = (P*N*R)/100= {2366*(3.5/12)*6/100} = ರೂ. 41.41

4.5 ಸಮಸ್ಯೆ 3: ಒಂದು ವರ್ಷದಲ್ಲಿ 100 ರೂ ಗಳಿಗೆ ತಿಂಗಳಿಗೆ 5 ರೂ ದರ(ಬಡ್ಡಿ)ದಂತೆ ಮೊತ್ತವು 1000 ಆದರೆ, ಅಸಲು ಮತ್ತು ಬಡ್ಡಿಯನ್ನು ಕಂಡು ಹಿಡಿ (ಲೀಲಾವತಿ ಶ್ಲೋಕ 92)

ಪರಿಹಾರ:

ಇಲ್ಲಿ,

A = 1000, R =60 N=1

ಆದರೆ, A = P{1+ (N*R)/100}

1000 = P{1+ (60*1)/100} = p*160/100 = 8/5

P = 1000*5/8 = 625 ರೂ.

ಸರಳ ಬಡ್ಡಿ SI = A-P = 1000-625 = ರೂ.375

4.5 ಸಮಸ್ಯೆ 4: ಮೂರು ಜನ ಅಕ್ಕ ತಂಗಿಯರ ವಯಸ್ಸು 5, 10 ಮತ್ತು15 ವರ್ಷಗಳು ಆಗಿರುವಾಗ ಅವರ ತಂದೆ ಬ್ಯಾಂಕ್ ನಲ್ಲಿ 5% ಸರಳ ಬಡ್ಡಿಯಲ್ಲಿ 80,250 ರೂಪಾಯಿಗಳನ್ನು ಇರಿಸಿದರು. ಮಕ್ಕಳಿಗೆ 20 ವರ್ಷಗಳಾದಾಗ, ಅವರಲ್ಲಿ ಪ್ರತಿಯೊಬ್ಬರಿಗೂ ಸಮ ಪಾಲು ಸಿಗುವಂತಾಗಬೇಕಾದರೆ, ತಂದೆ ಬ್ಯಾಂಕ್ ನಲ್ಲಿ ಇರಿಸಿದ ಹಣದಲ್ಲಿ ಪ್ರತಿ ಮಕ್ಕಳ ಪಾಲು ಎಷ್ಟು?

ಪರಿಹಾರ:

ಮಕ್ಕಳಿಗೆ 20 ವರ್ಷಗಳಾದಾಗ ಅವರೆಲ್ಲರೂ ಸಮಾನ ಹಣ ಪಡೆಯಬೇಕು. ಅದಕ್ಕೂ ಮೊದಲು ಈ ಹುಡುಗಿಯರ ಪಾಲುಗಳು ಕ್ರಮವಾಗಿ P₁,P₂ ,P₃ ಆಗಿರಲಿ.

ಬಡ್ಡಿ ದರ = 5%

ಹುಡುಗಿಯರ ವರ್ಷ	ಅವರ ಭಾಗ	ಬ್ಯಾಂಕಿನಲ್ಲಿ ಹಣ ಇರುವ ಕಾಲ (ಅವರಿಗೆ 20 ವರ್ಷವಾದಾಗ)	ಅಂತಿಮವಾಗಿ ಸಿಗುವ ಹಣ
5	P1	15 (5+15 =20)	=P1{1+ (N*R)/100} =P1{1+ (15*5)/100} =1.75 P1
10	P2	10 (10+10=20)	=P2 {1+ (N*R)/100} =P2 {1+ (10*5)/100} =1.5 P2
15	P3	5 (15+5 =20)	=P3{1+ (N*R)/100} =P3{1+ (5 *5)/100} =1.25 P3

ಅವರೆಲ್ಲರಿಗೆ 20 ವರ್ಷವಾದಾಗ ಸಿಗುವ ಹಣ ಸಮವೆಂದು ಕೊಟ್ಟಿದೆ.

1.75 P₁=1.5 P₂=1.25 P₃

ಸುಲಭ ರೂಪಕ್ಕೆ ತಂದಾಗ,(ಎಲ್ಲವನ್ನೂ 4 ರಿಂದ ಗುಣಿಸಿದಾಗ)

7P₁=6P₂=5P₃

P₂ = 7/6P₁

P₃ = 7/5P₁

ಆದರೆ P₁+P₂+P₃ = 80250

P₁+7/6P₁+7/5P₁= 80250

I.e. (30+35+42)/30 P₁= 80250

I.e. P₁= 80250*30/107 = 22500

ಈ ಬೆಲೆಗಳನ್ನ ಆದೇಶಿಸಿದಾಗ,

P₂ = 7/6P₁= 26250

P₃ = 7/5P₁= 31500

ತಂದೆ ಮೊದಲು ಇರಿಸಿದ 3 ಮಕ್ಕಳ ಪಾಲು ಹಣ: ರೂ.22,500, ರೂ.26,250 , ರೂ.31,500.

ಬಡ್ಡಿಯ ಸೂತ್ರ ಉಪಯೋಗಿಸಿ ಈ ಮೂರೂ ಜನರ ಹಣಗಳು ಅವರಿಗೆ 20 ವರ್ಷಗಳಾದಾಗ ಒಂದೇ ಮೊತ್ತ ಕೊಡುತ್ತದೋ ಎಂದು ತಾಳೆ ನೋಡಿ

4.5 ಕಲಿತ ಸಾರಾಂಶ

ಕ್ರ.ಸಂ.	ಕಲಿತ ಮುಖ್ಯಾಂಶಗಳು
1	ಸರಳ ಬಡ್ಡಿ (SI)= P*N*(R/100) ಇಲ್ಲಿ P = ಅಸಲು ಹಣ, N = ಅವಧಿ (ವರ್ಷ), R = ಬಡ್ಡಿಯದರ