5.2 ಅಂಕಿ ಅಂಶಗಳನ್ನು ನಕ್ಷೆಗಳ ಮೂಲಕ ಪ್ರತಿನಿಧಿಸುವ ವಿಧಾನ (Graphical representation of data)

ಸ್ತಂಭಾಲೇಖಾ(ಕಂಬಸಾಲಿನ ನಕ್ಷೆ) (Bar Chart)

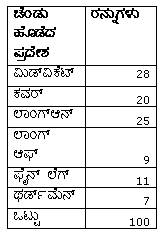
5.2 ಉದಾ 1: ನೀವು ಅಥವಾ ನಿಮ್ಮ ಸ್ನೇಹಿತ, ಕ್ರಿಕೆಟ್ ಆಡುವಾಗ ಒಂದು ಶಾಲಾ ಪಂದ್ಯದಲ್ಲಿ ರನ್ಗಳನ್ನು ಗಳಿಸುತ್ತೀರಿ. ಅಂತಹ ಪಂದ್ಯದಲ್ಲಿ ನೀವು ಶತಕ ಬಾರಿಸುತ್ತೀರಿ. ಇದಕ್ಕಾಗಿ ಚೆಂಡನ್ನು ವಿಕೆಟ್ ಸುತ್ತ ಎಲ್ಲಾ ಕಡೆಗೆ ಬಾರಿಸುತ್ತೀರಿ. ಆಗ ಚೆಂಡು ವಿಕೆಟ್ನ ಸುತ್ತ 6 ಪ್ರಮುಖ ಕೇಂದ್ರಗಳ ಮೂಲಕ ಹಾದು ಹೋಗಿರುತ್ತದೆ (ಮಿಡ್ ವಿಕೆಟ್, ಕವರ್, ಲಾಂಗ್ ಆನ್, ಲಾಂಗ್ ಆಫ್, ಫೈನ್ ಲೆಗ್ ಮತ್ತು ಥರ್ಡ್ಮೆನ್) ನೀವು ನೂರು ರನ್ಗಳನ್ನು ಗಳಿಸಿದ ರೀತಿ ಕೆಳಗಿನ ತಃಖ್ತೆಯಲ್ಲಿದೆ.

ಈಗ ಚೆಂಡು ಹೊಡೆದ ಪ್ರದೇಶ ಮತ್ತು ಗಳಿಸಿದ ರನ್ಗಳಿಗೆ ನಕ್ಷೆಯನ್ನು ಬಿಡಿಸುವಾ.

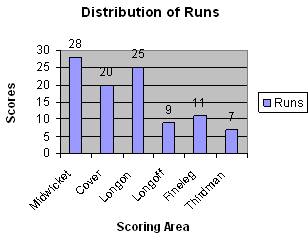
ಸ್ತಂಭಾಲೇಖ: (Bar Chart) ಮೇಲೆ ಸೂಚಿಸಿದ ಅಂಕಿ ಅಂಶಗಳನ್ನು ಬಲಗಡೆಯ ಚಿತ್ರದಲ್ಲಿರುವಂತೆ ಸೂಚಿಸಬಹುದು (ಸ್ತಂಭಾಲೇಖ ಅಥವಾ ಕಂಬಸಾಲು ನಕ್ಷೆ) ಲಂಬಸಾಲಿನಲ್ಲಿ 5 ರನ್ನುಗಳಿಗೆ 1 ಗುರುತು ಇದೆ. (0 ಯಿಂದ 30). ಚೆಂಡನ್ನು ಹೊಡೆದ ಸ್ಧಳಗಳ ಹೆಸರು ಅಡ್ಡ ಸಾಲಿನಲ್ಲಿದೆ. ಪ್ರತೀ ಸ್ಥಳವನ್ನು ಒಂದು ಸ್ತಂಭದಿಂದ ಸೂಚಿಸಿದೆ. ಸ್ತಂಭದ ಎತ್ತರವು ಆ ಪ್ರದೇಶದಲ್ಲಿ ಚೆಂಡನ್ನು ಹೊಡೆದಾಗ ಗಳಿಸಿದ ರನ್ನುಗಳ ಅನುಪಾತದಲ್ಲಿದೆ. ರನ್ ಹೆಚ್ಚಾದ ಹಾಗೆ ಸ್ಥಂಭದ ಎತ್ತರ ಹೆಚ್ಚಾಗುತ್ತದೆ. ಪ್ರತೀ ಸ್ತಂಭದ ಅಗಲ ಒಂದೇ ಸಮನಾಗಿದೆ. ಸ್ತಂಭಗಳ ಮಧ್ಯದ ಖಾಲಿ ಸ್ಥಳವೂ ಸಮನಾಗಿದೆ.

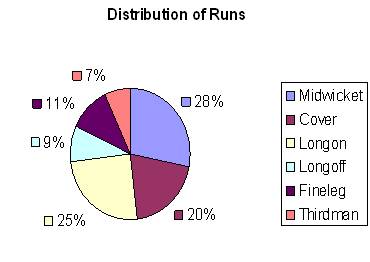
ಪೈ ನಕ್ಷೆ (Pie Chart) ಈಗ ನಾವು ಮೇಲಿನ ತಿಳಿಸಿದ ಅಂಕಿ ಅಂಶಗಳನ್ನು ಇನ್ನೊಂದು ಹೊಸ ಮಾದರಿಯ ನಕ್ಷೆಯಲ್ಲಿ ನಿರೂಪಿಸುವಾ. ಇದನ್ನು ಪೈ ನಕ್ಷೆ ಎನ್ನುವರು. (ಚಿತ್ರನೋಡಿ). ಇಲ್ಲಿ ರನ್ನು ಗಳಿಸಿದ ಪ್ರತೀ ಪ್ರದೇಶವನ್ನು ವಿವಿಧ ಬಣ್ಣಗಳಿಂದ ಸೂಚಿಸಿದೆ. ಇಲ್ಲಿ ರನ್ನು ಸಂಖ್ಯೆಯನ್ನು 360^0 ಕೋನದ ಶೇಕಡಾ ಪರಿಣಾಮವಾಗಿ ಪರಿವರ್ತಿಸಿ, ವೃತ್ತ ಖಂಡಗಳನ್ನೆಳೆದಿದೆ. ಪ್ರತೀ ವೃತ್ತ ಖಂಡವೂ ಒಂದೊಂದು ಪ್ರದೇಶದಲ್ಲಿ ಗಳಿಸಿದ ರನ್ನುಗಳ ಅನುಪಾತದಲ್ಲಿದೆ. ಶೇಕಡಾ ಪ್ರಮಾಣ ಹೆಚ್ಚಾದಷ್ಟು, ವೃತ್ತ ಖಂಡದ ಗಾತ್ರ ಹೆಚ್ಚಾಗುತ್ತದೆ.

ಈ ಮೇಲಿನ ಎರಡು ನಕ್ಷೆಗಳನ್ನು ಹೋಲಿಸಿದಾಗ, ಈ ಉದಾಹರಣೆಯಲ್ಲಿ ಪೈ ನಕ್ಷೆಯು ಸ್ತಂಭಾಲೇಖಕ್ಕಿಂತ ಹೆಚ್ಚು ಸೂಕ್ತ ಎನಿಸುವುದಿಲ್ಲವೆ?

ಏಕೆ?

ನೀಡಿದ ಅಂಕಿ ಅಂಶಗಳನ್ನು ಶೇಕಡಾವಾರು ಪರಿವರ್ತಿಸಲು ಆಗದಿದ್ದರೆ ಸ್ತಂಭಾಲೇಖ ಸೂಕ್ತ(ಉದಾ: ದತ್ತ ಅಂಶಗಳು ಬೇರೆ ದೇಶಗಳಿಗೆ ಅಥವಾ ಬೇರೆ ಬೇರೆ ವರ್ಷಗಳಿಗೆ ಸಂಬಂಧಿಸಿದಾಗ) ನೀಡಿದ ಅಂಕಿ ಅಂಶಗಳನ್ನು ಶೇಕಡಾವಾರು ಪರಿವರ್ತಿಸಲು ಆಗುವುದಾದರೆ ಪೈ ನಕ್ಷೆಯೇ ಸೂಕ್ತ.

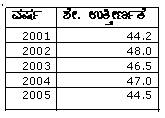
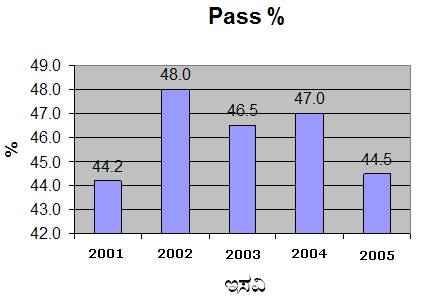
5.2 ಉದಾ 2: ಕೆಳಗೆ ತ:ಖ್ತೆಯಲ್ಲಿ ಕೊಟ್ಟಿರುವ ಅಂಶಗಳು ಒಂದು ಮಂಡಳಿಯ ಪರೀಕ್ಷೆಯಲ್ಲಿ ಕೆಲವು ವರ್ಷಗಳಲ್ಲಿನ ಶೇಕಡಾ ಉತ್ತೀರ್ಣತೆಯನ್ನು ತೋರಿಸುತ್ತದೆ.

ಪರಿಹಾರ:

ಪಕ್ಕದ ಚಿತ್ರದಲ್ಲಿ ಶೇಕಡಾ ಉತ್ತೀರ್ಣತೆಯನ್ನು 0 ಯ ಬದಲಾಗಿ 42 ರಿಂದ ಆರಂಭಿಸಿದ್ದೇವೆ. ಏಕೆ? (ಸೊನ್ನೆಯಿಂದ ಆರಂಭಿಸಿದರೆ ನಕ್ಷೆ ತುಂಬಾ ಉದ್ದವಾಗುತ್ತದೆ.)

ಸ್ತಂಭಾಲೇಖ ಮತ್ತು ಪೈ ನಕ್ಷೆಯ ರಚನೆ (Construction of Bar and Pie charts)

5.2. ಉದಾ 3: ಮಾನವನ ಹೃದಯ ಬಡಿತದ ವಿವರಗಳನ್ನು ಕೊಟ್ಟಿದೆ. ಸೂಕ್ತವಾದ ಪ್ರಮಾಣ ಉಪಯೋಗಿಸಿ ನಕ್ಷೆ ರಚಿಸಿ:-

ಪ್ರಾಯ (ವರ್ಷಗಳಲ್ಲಿ) à	5	10	12	15	18 ರ ಮೇಲೆ
ಹೃದಯ ಬಡಿತ(ನಿಮಿಷಕ್ಕೆ) à	100	92	85	80	72

ಪರಿಹಾರ:

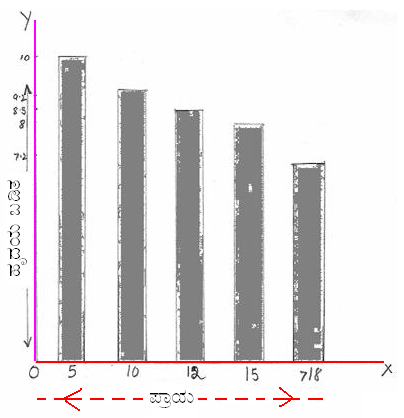
ಇಲ್ಲಿ ಹೃದಯ ಬಡಿತದ ಸಂಖ್ಯೆಗಳನ್ನು ಶೇಕಡಾ ಪ್ರಮಾಣದಲ್ಲಿ ನಿರೂಪಿಸಲು ಸಾಧ್ಯವಿಲ್ಲ. ಆದ್ದರಿಂದ ಅಂಕಿ ಅಂಶಗಳಿಗೆ ಸೂಕ್ತವಾದ ನಕ್ಷೆ ‘ಸ್ತಂಭಾಲೇಖ’.

ಹಂತ 1. ಒಂದು ಖಾಲಿ ಹಾಳೆ ಅಥವಾ ನಕ್ಷಾಕಾಗದ(ಗ್ರಾಫ್ ಹಾಳೆ)ದಲ್ಲಿ ಒಂದು ಅಡ್ಡಗೆರೆ ‘OX’ ಹಾಕಿ. ಹಂತ 2. O ಬಿಂದುವಿನಲ್ಲಿ OX ಗೆ ಲಂಬವಾಗಿ OY ರೇಖೆ ಎಳೆಯಿರಿ. OX ರೇಖೆಯು ಮಾನವನ ವಯಸ್ಸನ್ನು ಸೂಚಿಸುತ್ತದೆ. OY ರೇಖೆಯು ಹೃದಯ ಬಡಿತದ ಸಂಖ್ಯೆಗಳನ್ನು ಸೂಚಿಸುತ್ತದೆ. ಹಂತ 3. ಹೃದಯ ಬಡಿತ 72 ರಿಂದ 100ರವರೆಗೆ ಇದೆ. ಆದ್ದರಿಂದ ಪ್ರಮಾಣ 1 ಸೆ.ಮಿ. = 10 ಬಡಿತ ಎಂದಿಟ್ಟುಕೊಳ್ಳಿ. ಆಗ, 100 ಬಡಿತ =  100*1/10 = 10 ಸೆ.ಮಿ 92 ಬಡಿತ =   92*1/10 = 9.2 ಸೆ.ಮಿ 85   ಬಡಿತ = 85*1/10   = 8.5 ಸೆ.ಮಿ 80   ಬಡಿತ = 80*1/10  =  8 ಸೆ.ಮಿ 72   ಬಡಿತ = 72*1cm/10  = 7.2 ಸೆ.ಮಿ ಇವುಗಳು ಸ್ತಂಭಗಳ ಎತ್ತರಗಳಾಗಿವೆ. ಹಂತ 4. ‘OX’ ರೇಖೆಯ ಮೇಲೆ O ದಿಂದ ಸುಮಾರು 1.5 ಸೆ.ಮಿ. ದೂರದಲ್ಲಿ è ‘5’ ನ್ನು ಗುರುತಿಸಿ (ಇದು ವಯಸ್ಸು 5 ನ್ನು ಸೂಚಿಸುತ್ತದೆ) ಹಂತ 5. ‘5’ರ ಮೇಲೆ 10ಸೆ.ಮಿ. ಎತ್ತರ (=100 ಬಡಿತ) ಮತ್ತು 1 ಸೆ.ಮಿ. ಅಗಲದ ಒಂದು ಸ್ತಂಭದಿಂದ ರಚಿಸಿ. ಈ ಸ್ತಂಭವು 5 ವರ್ಷ ಪ್ರಾಯದವನ ಹೃದಯ ಬಡಿತವನ್ನು ಸೂಚಿಸುತ್ತದೆ. ಹಂತ 6. ಈ ಸ್ತಂಭದಿಂದ ಸುಮಾರು 1.5 ಸೆ.ಮಿ. ದೂರದಲ್ಲಿ ‘10’ ನ್ನು ಗುರುತಿಸಿ. (ಇದು ವಯಸ್ಸು 10ನ್ನು ಸೂಚಿಸುತ್ತದೆ). ಹಂತ 7. ‘10’ರ ಮೇಲೆ 9.2ಸೆ.ಮಿ (=92 ಬಡಿತ) ಎತ್ತರದ, 1ಸೆ.ಮಿ. ಅಗಲದ ಒಂದು ಸ್ತಂಭವನ್ನು ರಚಿಸಿ. ಈ ಸ್ತಂಭವು 10 ವರ್ಷ ಪ್ರಾಯದವನ ಹೃದಯ ಬಡಿತವನ್ನು ಸೂಚಿಸುತ್ತದೆ. ಹಂತ 8. 6 ಮತ್ತು 7 ನೇ ಹಂತಗಳಲ್ಲಿ ಮಾಡಿದ ಕ್ರಿಯೆಯನ್ನು ಉಳಿದ ಪ್ರಾಯಗಳಾದ 12, 15 ಮತ್ತು ‘>18’ ಕ್ಕೂ ಮಾಡಿ. (8.5ಸೆ.ಮಿ., 8ಸೆ.ಮಿ. ಮತು 7.2ಸೆ.ಮಿ.ಸ್ತಂಭ ರಚಿಸಿ) ಪ್ರತೀ ಸ್ತಂಭದ ಅಗಲ ಒಂದೇ ಆಗಿರಲಿ (1ಸೆ.ಮಿ.).

5.2 ಉದಾ 4: 250 ವಿದ್ಯಾರ್ಥಿಗಳಲ್ಲಿ ದೂರದರ್ಶನದ ಬೇರೆ ಬೇರೆ ಚಾನೆಲ್ಗಳನ್ನು ವೀಕ್ಷಿಸಲು ಇಷ್ಟ ಪಡುವವರ ವಿವರಣೆ ಪಟ್ಟಿ ಕೆಳಗಿದೆ. ಇದಕ್ಕೆ ಸೂಕ್ತವಾದ ನಕ್ಷೆ ರಚಿಸಿ.

	ಚಾನೆಲ್ಗಳು	ವಿದ್ಯಾರ್ಥಿಗಳು
1	ನ್ಯಾಶನಲ್ ಜಿಯೊಗ್ರಾಫಿಕ್	100
2	ಡಿಸ್ಕವರಿ ಚಾನೆಲ್	50
3	ಸ್ಪೋಟ್ರ್ಸ್ ಚಾನೆಲ್	75
4	ಇತರ	25

ಪರಿಹಾರ:

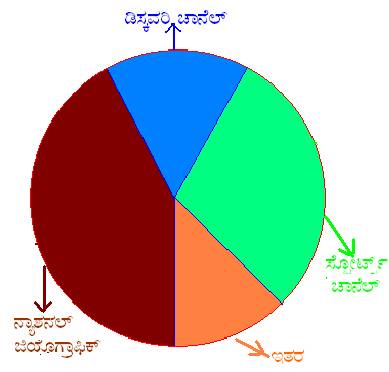
ಒಟ್ಟು ವಿದ್ಯಾರ್ಥಿಗಳ ಸಂಖ್ಯೆ 250 ಇದ್ದು, ಪ್ರತೀ ಚಾನೆಲ್ನ್ನು ವೀಕ್ಷಿಸುವ ವಿದ್ಯಾರ್ಥಿಗಳ ಸಂಖ್ಯೆಯನ್ನು ಶೇಕಡಾ ಪ್ರಮಾಣದಲ್ಲಿ ಹೇಳಬಹುದು. ಆದ್ದರಿಂದ ಇಲ್ಲಿ ಪೈ ನಕ್ಷೆ ಸೂಕ್ತವಾಗಿದೆ.

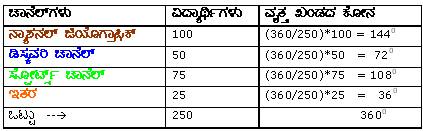
ಹಂತ 1 : ನಾಲ್ಕು ವಿಧದ, ವಿದ್ಯಾರ್ಥಿಗಳ ಸಂಖ್ಯೆಗಳಿಗೆ ಅನುಗುಣವಾದ ವೃತ್ತ ಖಂಡದ ಗಾತ್ರ ಕಂಡುಹಿಡಿಯಿರಿ. ವಿ.ಸೂ: ವೃತ್ತ ಕೇಂದ್ರದಲ್ಲುಂಟಾಗುವ ಕೋನ 360^0. ನಾವು ವಿದ್ಯಾರ್ಥಿಗಳ ಸಂಖ್ಯೆಯನ್ನು 360 ರಿಂದ ಗುಣಿಸಿ, ಒಟ್ಟು ವಿದ್ಯಾರ್ಥಿಗಳ ಸಂಖ್ಯೆಯಿಂದ ಭಾಗಿಸಿ ವೃತ್ತ ಖಂಡದ ಗಾತ್ರ ನೋಡಿದೆವು. ಹಂತ 2. ಅನುಕೂಲವಾದ ತ್ರಿಜ್ಯದಿಂದ ಒಂದು ವೃತ್ತ ರಚಿಸಿ. ಹಂತ 3. ವೃತ್ತ ಕೇಂದ್ರದಲ್ಲಿ ಮೇಲಿನ ಕೋನಗಳಾಗುವಂತೆ ಗುರುತಿಸಿ, ಅನುಕ್ರಮವಾದ ವೃತ್ತ ಖಂಡಗಳನ್ನು ರಚಿಸಿ. ಹಂತ 4. ಪ್ರತೀ ವೃತ್ತ ಖಂಡಕ್ಕು ಬೇರೆ ಬೇರೆ ಬಣ್ಣಗಳನ್ನು ಕೊಟ್ಟು, ಆವೃತ್ತ ಖಂಡಗಳೊಳಗೆ ಅವುಗಳಿಗನುಸಾರವಾದ ಟಿ.ವಿ. ಚಾನೆಲುಗಳ ಹೆಸರು ಬರೆಯಿರಿ.

5.2 ಉದಾ 5: ಒಂದು ಶಾಲೆಯ 10^ನೇ ತರಗತಿಯಲ್ಲಿ 4 ವಿಭಾಗಗಳಿದ್ದು, ಅವುಗಳಲ್ಲಿ ಕಲಿಯುತ್ತಿರುವ ವಿದ್ಯಾರ್ಥಿಗಳ ಸಂಖ್ಯೆಯನ್ನು ಕೆಳಗೆ ನೀಡಿದೆ.

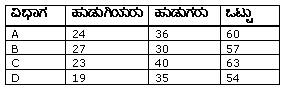
ಅಲ್ಲಿನ ಅಂಕಿ ಅಂಶಗಳನ್ನು ಸೂಕ್ತವಾದ ಪ್ರಮಾಣ ನಕ್ಷೆಯಿಂದ ತೋರಿಸಿ.

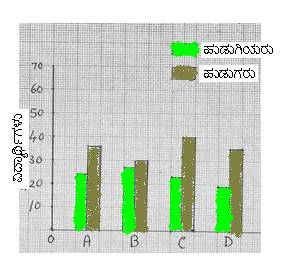
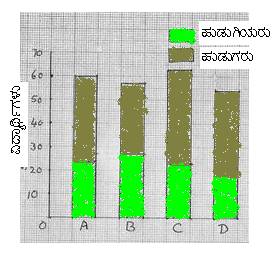
ಈ ಸಮಸ್ಯೆಗೆ ನಾವು 2 ಬೇರೆ ಬೇರೆ ಕಂಬಸಾಲು ನಕ್ಷೆಗಳನ್ನು ರಚಿಸಬಹುದು.(ಒಂದು ಹುಡುಗರಿಗೆ, ಇನ್ನೊಂದು ಹುಡುಗಿಯರಿಗೆ) ಎರಡರ ಬದಲು ಎಡಗಡೆ ಚಿತ್ರದಲ್ಲಿ ತೋರಿಸಿದಂತೆ ಅಂಕಿ ಅಂಶಗಳನ್ನು ಒಂದರ ಪಕ್ಕದಲ್ಲಿ ಇನ್ನೊಂದು ನಮೂದಿಸಿದಾಗ ಅಧ್ಯಯನ ಸುಲಭ. ಈ ರೀತಿಯ ನಕ್ಷೆಯನ್ನು Joint Bar chart ಎಂದು ಕರೆಯುತ್ತಾರೆ. ಬಲಗಡೆ ಚಿತ್ರದಲ್ಲಿ ಇರುವುದನ್ನು ‘Sub-divided bar chart’  ಎಂದು ಕರೆಯುತ್ತಾರೆ.

5.2 ಕಲಿತ ಸಾರಾಂಶ

ಕ್ರ.ಸಂ.	ಕಲಿತ ಮುಖ್ಯಾಂಶಗಳು
1	ಸ್ತಂಭ ನಕ್ಷೆಯು ದತ್ತಾಂಶಗಳನ್ನು ಸಮಾನ ಅಗಲದ ಸ್ತಂಭಗಳ ಮೂಲಕ ಸೂಚಿಸುವ ಕ್ರಮ. ಸ್ತಂಭದ ಎತ್ತರವು ದತ್ತಾಂಶ ಸಂಖ್ಯೆಗೆ ಅನುಗುಣವಾಗಿರುತ್ತದೆ.
2	ಪೈನಕ್ಷೆಯು ದತ್ತಾಂಶಗಳನ್ನು ಒಂದು ವೃತ್ತ ಖಂಡಗಳಾಗಿ ನಿರೂಪಿಸುವ ಕ್ರಮ ವೃತ್ತ ಖಂಡದ ಗಾತ್ರವು ದತ್ತಾಂಶ ಸಂಖ್ಯೆಗಳಿಗೆ ಅನುಗುಣವಾಗಿರುತ್ತದೆ.