6.3 Theorem
on Parallel lines:
‘Theorem’ is a proposition in
which some statements are to be proved logically.
Theorem has following parts;
1. Data(Hypothesis) - Lists the facts given in the theorem.
2. Figure relevant for the theorem
3. To prove- The statement or proposition which is
to be proved
4. Construction if any(More
details added to the figure drawn in
step 2)
5. Proof (Series of several steps)
An example of a theorem which will be
proved later is:
|
Pythagoras’s theorem: Square of hypotenuse in a right angled triangle is equal to sum
of squares of other two sides (Hypotenuse)2 = (Side)2 + (Side)2 |
|
Theorem can not be proved by just by giving several
examples. It needs to be proved by one of the following two methods:
1. Based on axioms or theorems already proved.
2. Some theorems are proved by negation (we start
with the assumption that theorem is wrong and then arrive at a contradiction or
mathematical absurdity. This forces
us to arrive at a conclusion that our assumption was wrong and hence theorem
must be true).
However, to disprove a statement, an
example which does not satisfy the given statement will be enough.
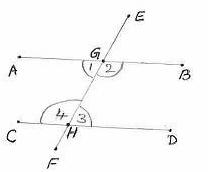
6.3 Theorem 1: If a transversal line cuts two parallel lines then
1) Each pair of alternate angles is equal
2) The interior angles on the same side of the
transversal are supplementary
Data: AB || CD, Transversal EF cuts AB at G and CD
at H
To prove:
1) ![]() AGH =
AGH = ![]() GHD,
GHD, ![]() BGH=
BGH=![]() CHG
CHG
2) ![]() AGH+
AGH+![]() CHG = 1800,
CHG = 1800, ![]() BGH+
BGH+![]() DHG =1800
DHG =1800
|
No |
Statement |
Reason |
|
|
1 |
|
Enunciation
3 : Corresponding angles are equal when a transversal cuts parallel lines |
|
|
2 |
|
Enunciation
2 : vertically opposite angles are equal |
|
|
3 |
|
Axiom
1 for angles in steps 1 and 2 Things
which are equal to the same thing are equal to each other |
|
|
4 |
|
Enunciation
3: Corresponding angles |
|
|
5 |
|
Enunciation
2: Vertically opposite angle |
|
|
6 |
|
Axiom
1 for angles in step 4 and 5 |
|
|
7 |
|
Enunciation
1 : The ray FE is standing on the
straight line AB |
|
|
8 |
|
From
Step 6 |
|
|
9 |
|
Substitute
|
|
|
10 |
|
Enunciation1
: The ray FE is standing on the
straight line CD |
|
|
11 |
|
From
step 6 |
|
|
12 |
|
Substitute
|
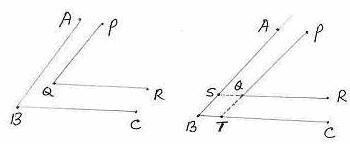
6.3 Problem 1: In the figure AB || PQ and BC || QR. Prove that ![]() PQR =
PQR =![]() ABC
ABC
Data: AB ||
PQ and BC || QR
To Prove: ![]() PQR =
PQR =![]() ABC
ABC
Construction: Extend PQ to cut BC at T, Extend QR to cut AB
at S
Proof:
|
|
|
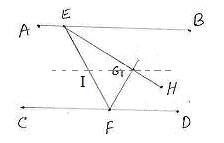
6.3 Problem 2: In the adjacent
figure, AB||CD. EH and FG are the angular bisectors of ![]() FEB and
FEB and ![]() EFD respectively.
EFD respectively.
Prove that EH and FG are
perpendicular to each other.
Construction: Draw GI
parallel to CD passing through G
Solution:
|
No |
Statement |
Reason |
|
|
1 |
|
Alternate angles: AB ||CD |
|
|
2 |
|
Given that EH bisects |
|
|
3 |
|
Equality of Step 1 and 2 |
|
|
4 |
|
Alternate angles: AB ||CD |
|
|
5 |
|
Given that GF bisects |
|
|
6 |
|
Angles on a straight line CD |
|
|
7 |
2 |
Substitute 3 and 5 in 6 |
|
|
8 |
|
Simplification of 7 |
|
|
9 |
|
EG bisects |
|
|
10 |
|
Alternate angles AB||IG |
|
|
11 |
|
Equate 9 and 10 |
|
|
12 |
|
FG bisects |
|
|
13 |
|
Alternate angles CD||IG |
|
|
14 |
|
Equate 12 and 13 |
|
|
15 |
|
Substituting 11 and 14 in 8 |
|
|
16 |
Thus EH and FG are perpendicular
to each other |
||
6.3 Summary of learning
|
No |
Points to remember |
|
1 |
If
a transversal line cuts two parallel lines then 1)
Each pair of alternate angles are equal 2)
The interior angles on the same side of the transversal are supplementary |
Additional Points:
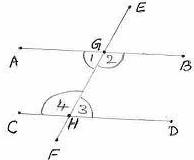
6.3 Theorem 2(Converse of the theorem 6.3.1): If a transversal line
cuts two straight lines such that
Case1): Each pair of alternate angles is equal
OR
Case 2): The interior angles on the same side of
the transversal are supplementary
Then the straight lines are parallel.
Given:
1) Transversal EF cuts two straight lines AB and CD
at G and H respectively. And
2) ![]() AGH =
AGH = ![]() GHD (
GHD (![]() BGH=
BGH=![]() CHG)
CHG)
OR
3) ![]() AGH +
AGH +![]() CHG = 1800 (
CHG = 1800 (![]() BGH +
BGH +![]() DHG = 1800)
DHG = 1800)
TO prove: AB||CD.
|
Hint: In
both the cases show that the corresponding angles are equal and then use the
enunciation ‘6.1.3 Enunciation 4’ to show that these lines are parallel |
|
.