6.3 ಸಮಾಂತರ ಸರಳರೇಖೆಗಳ ಮೇಲಿನ ಪ್ರಮೇಯ (Theorem on Parallel lines):

ತರ್ಕಬದ್ಧವಾಗಿ ಸಾಧಿಸಬೇಕಾದ ಹೇಳಿಕೆಗಳನ್ನು ‘ಪ್ರಮೇಯ’ (Theorem) ಎನ್ನುವರು.

ಒಂದು ಪ್ರಮೇಯದಲ್ಲಿ ಈ ಕೆಳಗಿನ ಭಾಗಗಳಿರುತ್ತವೆ:-

1. ದತ್ತ: ಪ್ರಮೇಯದಲ್ಲಿ ಕೊಟ್ಟ ಅಂಶಗಳು.

2. ಪ್ರಮೇಯದ ದತ್ತಾಂಶಕ್ಕನುಗುಣವಾದ ಒಂದು ನಕ್ಷೆ(ಚಿತ್ರ).

3. ಸಾಧನೀಯ: ಸಾಧಿಸಬೇಕಾದ ಅಂಶಗಳು.

4. ರಚನೆ: ಪ್ರಮೇಯದ ಸಾಧನೆಗೆ ಹೆಚ್ಚಿನ ರಚನೆ ಬೇಕಾದರೆ, ಅವುಗಳ ರಚನೆ.

5. ಸಾಧನೆ: ತರ್ಕಬದ್ಧವಾದ ಸಾಧನೆ.

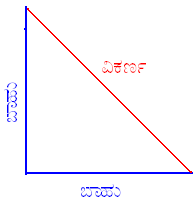
‘ಪ್ರಮೇಯ’ಕ್ಕೆ ಒಂದು ಉದಾಹರಣೆ: ಪೈಥಾಗೊರಸನ ಪ್ರಮೇಯ: “ಒಂದು ಲಂಬಕೋನ ತ್ರಿಕೋನದಲ್ಲಿ ವಿಕರ್ಣದ ವರ್ಗವು ಉಳಿದೆರಡು ಬಾಹುಗಳ ವರ್ಗಗಳ ಮೊತ್ತಕ್ಕೆ ಸಮ”. (ವಿಕರ್ಣ)^2 = (ಬಾಹು)^2+(ಬಾಹು)^2 ಇದನ್ನು ಮುಂದೆ ಸಾಧಿಸಲಿಕ್ಕೆ ಇದ್ದೇವೆ.

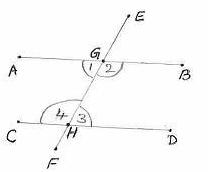
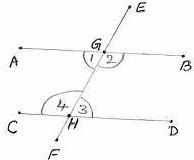
6.3 ಪ್ರಮೇಯ 1: ಎರಡು ಸಮಾಂತರ ಸರಳರೇಖೆಗಳನ್ನು ಒಂದು ಛೇದಕರೇಖೆಯು ಛೇದಿಸಿದಾಗ ಉಂಟಾಗುವ

1. ಪ್ರತಿಯೊಂದು ಜೊತೆ ಪರ್ಯಾಯ ಕೋನಗಳು ಸಮವಾಗಿರುತ್ತವೆ.

2. ಛೇದಕ ರೇಖೆಯ ಒಂದೇ ಪಾರ್ಶ್ವದಲ್ಲಿರುವ ಅಂತರ್ಕೋನಗಳು ಪರಿಪೂರಕಗಳಾಗಿರುತ್ತವೆ.

ದತ್ತ: AB || CD, EF ಇಈ ಛೇದಕ ರೇಖೆಯು AB ಮತ್ತು CD ಗಳನ್ನು ಕ್ರಮವಾಗಿ G ಮತ್ತು H ಗಳಲ್ಲಿ ಛೇದಿಸಿದೆ.

ಸಾಧನೀಯ:

1) AGH = GHD, BGH=CHG (1 = 3, 2=4)

2) AGH+CHG = 180⁰, BGH+DHG =180⁰(1+4 = 180⁰, 2+3 =180⁰)

ಸಂ.	ನಿರೂಪಣೆ	ಕಾರಣಗಳು
1	EGB = GHD
2	EGB = AGH	ಶೃಂಗಾಭಿಮುಖ ಕೋನಗಳು ಸಮ
3	AGH = GHD	ಸ್ವಯಂಸಿದ್ಧ 1: ಒಂದೇ ಅಂಶಕ್ಕೆ ಸಮನಾದ ಅಂಶಗಳು ಪರಸ್ಪರ ಸಮ.
4	AGE =CHG	ಅನುರೂಪಕೋನಗಳು ಸಮ
5	AGE = BGH	ಶೃಂಗಾಭಿಮುಖ ಕೋನಗಳು ಸಮ
6	CHG=BGH	ಸ್ವಯಂಸಿದ್ಧ 1: ಒಂದೇ ಅಂಶಕ್ಕೆ ಸಮನಾದ ಅಂಶಗಳು ಪರಸ್ಪರ ಸಮ.
7	AGH+HGB= 180^0	ಸರಳಯುಗ್ಮ ಕೋನಗಳು
8	BGH = CHG	ಹಂತ 5, 6 ರಿಂದ
9	AGH+CHG= 180^0	HGB ಯ ಬದಲು CHG ಯನ್ನು ಆದೇಶಿಸಿದೆ.
10	CHG +GHD = 180^0	ಸರಳಯುಗ್ಮ ಕೋನಗಳು
11	BGH = CHG	ಹಂತ 6 ರಿಂದ
12	GHD+BGH= 180^0	10 ರಲ್ಲಿ CHG ಬದಲು BGH ಆದೇಶಿಸಿದೆ.

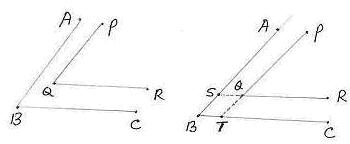
6.3 ಸಮಸ್ಯೆ 1: ಕೆಳಗಿನ ಚಿತ್ರದಲ್ಲಿ AB || PQ ಮತ್ತು BC || QR, ಆದರೆ PQR =ABC ಎಂದು ಸಾಧಿಸಿ

ದತ್ತ :  AB || PQ, BC || QR

ಸಾಧನೀಯ: PQR =ABC

ರಚನೆ: PQ ವನ್ನ ವೃದ್ಧಿಸಿದೆ. ಅದು BC ಯನ್ನು T ನಲ್ಲಿ ಛೇದಿಸಿದೆ. RQ ವನ್ನ ವೃದ್ಧಿಸಿದೆ. ಅದು AB ಯನ್ನು S ನಲ್ಲಿ ಛೇದಿಸಿದೆ.

ಸಾಧನೆ:

PQR = ASR (AB || PQ : ಅನುರೂಪ ಕೋನಗಳು) ASR = ABC (BC || QR : ಅನುರೂಪ ಕೋನಗಳು) PQR =ABC

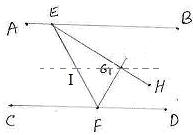
6.3 ಸಮಸ್ಯೆ 2 : ಚಿತ್ರದಲ್ಲಿ AB||CD. EH ಮತ್ತು FG ಗಳು ಕ್ರಮವಾಗಿ FEB ಮತ್ತು EFD ಗಳ ಕೋನಾರ್ಧಕ ರೇಖೆಗಳು.

ಆಗ, EH ಮತ್ತು FG ಗಳು ಪರಸ್ಪರ ಲಂಬವಾಗಿವೆ ಎಂದು ಸಾಧಿಸಿ

ರಚನೆ: CD ಗೆ ಸಮಾಂತರವಾಗಿ G ಬಿಂದುವಿನ ಮೂಲಕ GI ರೇಖೆಯನ್ನೆಳೆದಿದೆ.

ಪರಿಹಾರ:

ಸಂ.	ನಿರೂಪಣೆ	ಕಾರಣಗಳು
1	CFE = BEF	AB ||CD ಪರ್ಯಾಯ ಕೋನಗಳು.
2	BEF = 2FEG	FEB ಯ ಕೋನಾರ್ಧಕ EH.
3	CFE = 2FEG	1 ಮತ್ತು 2 ರಿಂದ .
4	EFD = AEF	AB ||CD ಪರ್ಯಾಯ ಕೋನಗಳು.
5	EFD = 2EFG	EFD ಯ ಕೋನಾರ್ಧಕ GF.
6	CFE +EFD = 180^0	CD ರೇಖೆಯ ಮೇಲಿನ ಕೋನಗಳು (ಸರಳಯುಗ್ಮ)
7	2FEG +2EFG = 180^0	3 ಮತ್ತು 5 ರಿಂದ 6ರಲ್ಲಿ ಆದೇಶಿಸಿದೆ .
8	FEG +EFG = 90^0	7 ನ್ನ ಸುಲಭೀಕರಿಸಿದೆ .
9	FEG = GEB	BEI ಯ ಕೋನಾರ್ಧಕ EG
10	GEB = EGI	AB||IG ಪರ್ಯಾಯ ಕೋನಗಳು .
11	FEG = EGI	ಮತ್ತು 10 ರಿಂದ
12	EFG=GFD	IFD ಯ ಕೋನಾರ್ಧಕ FG
13	GFD =IGF	CD||IG ಪರ್ಯಾಯ ಕೋನಗಳು.
14	EFG =IGF	12 ಮತ್ತು 13ರಿಂದ .
15	EGI +IGF(=EGF) = 90^0	11 ಮತ್ತು 14 ರಿಂದ 8ರಲ್ಲಿ ಆದೇಶಿಸಿದೆ .
16	ಆದ್ದರಿಂದ , EH ಮತ್ತು FG ಗಳು ಪರಸ್ಪರ ಲಂಬವಾಗಿವೆ .

6.3 ಪ್ರಮೇಯ 2(1ನೇ ಪ್ರಮೇಯದ ವಿಲೋಮ): ಎರಡು ಸಮಾಂತರ ಸರಳರೇಖೆಗಳನ್ನು ಒಂದು ಛೇದಿಸಿದಾಗ,

1): ಪ್ರತಿಯೊಂದು ಜೊತೆ ಪರ್ಯಾಯ ಕೋನಗಳು ಸಮವಾಗಿದ್ದರೆ

ಅಥವಾ

2): ಛೇದಕ ರೇಖೆಯ ಒಂದೇ ಪಾರ್ಶ್ವದಲ್ಲಿನ ಅಂತರ್ ಕೋನಗಳು ಪರಿಪೂರಕಗಳಾಗಿದ್ದರೆ, ಪಾರ್ಶ್ವದಲ್ಲಿನ

ಆ ಎರಡು ಸರಳ ರೇಖೆಗಳು ಸಮಾಂತರ ರೇಖೆಗಳಾಗಿರುತ್ತವೆ.

ದತ್ತ:

‘1) AB ಮತ್ತು CD ಸರಳರೇಖೆಗಳನ್ನು EF ಛೇದಿಸುತ್ತದೆ ಮತ್ತು 2) AGH = GHD (BGH=CHG) ಅಥವಾ 3) AGH+CHG = 180^0(BGH+DHG =180^0) ಸಾಧನೀಯ:   AB||CD. ಸೂಚನೆ: ಮೊದಲು ಅನುರೂಪ ಕೋನಗಳು ಸಮವೆಂದು ಸಾಧಿಸಿ. ನಂತರ 6.2.3 ಹೇಳಿಕೆ 4 ರ ಆಧಾರದಂತೆ ರೇಖೆಗಳು ಸಮಾಂತರವಾಗಿರುತ್ತವೆ

6.3 ಕಲಿತ ಸಾರಾಂಶ

ಸಂ	ಕಲಿತ ಮುಖ್ಯಾಂಶಗಳು
1	ಎರಡು ಸಮಾಂತರ ಸರಳರೇಖೆಗಳನ್ನು ಒಂದು ರೇಖೆಯು ಛೇದಿಸಿದಾಗ ಉಂಟಾಗುವ 1) ಪ್ರತಿಯೊಂದು ಜೊತೆ ಪರ್ಯಾಯ ಕೋನಗಳು ಸಮವಾಗಿರುತ್ತವೆ. 2) ಛೇದಕ ರೇಖೆಯ ಒಂದೇ ಪಾರ್ಶ್ವದಲ್ಲಿನ ಅಂತರ್ ಕೋನಗಳು ಪರಿಪೂರಕಗಳಾಗಿರುತ್ತವೆ.
2	ಎರಡು ಸಮಾಂತರ ಸರಳರೇಖೆಗಳನ್ನು ಒಂದು ರೇಖೆಯು ಛೇದಿಸಿದಾಗ, 1): ಪ್ರತಿಯೊಂದು ಜೊತೆ ಪರ್ಯಾಯ ಕೋನಗಳು ಸಮವಾಗಿದ್ದರೆ ಅಥವಾ 2): ಛೇದಕ ರೇಖೆಯ ಒಂದೇ ಪಾರ್ಶ್ವದಲ್ಲಿನ ಅಂತರ್ ಕೋನಗಳು ಪರಿಪೂರಕಗಳಾಗಿದ್ದರೆ, ಆ ಎರಡು ಸರಳ ರೇಖೆಗಳು ಸಮಾಂತರ ರೇಖೆಗಳಾಗಿರುತ್ತವೆ.