6.6 ಬಹುಭುಜಾಕೃತಿಗಳು(ಸಮತಲಾಕೃತಿಗಳು) Polygons (Rectilinear figures):
ಕೆಳಗೆ ಕೊಟ್ಟ ಚಿತ್ರಗಳನ್ನು ಗಮನಿಸಿ.

ಎಲ್ಲವೂ ಒಂದೇ ಸಮತಲದಲ್ಲಿವೆ.
ಎಲ್ಲವೂ ಆವೃತ ಆಕೃತಿಗಳು.
ಎಲ್ಲವೂ 3 ಅಥವಾ ಹೆಚ್ಚು ರೇಖಾಖಂಡಗಳಿಂದ ಸುತ್ತುವರಿಯಲ್ಪಟ್ಟಿವೆ.
ಎಲ್ಲಾ ಆಕೃತಿಗಳಲ್ಲೂ 3 ಅಥವಾ ಹೆಚ್ಚು ಸಂಧಿಸುವ ಬಿಂದುಗಳಿವೆ.
ವ್ಯಾಖ್ಯೆ:
ಒಂದೇ ಸಮತಲದಲ್ಲಿರುವ, ಸರಳರೇಖೆ ಆಗಿರದ ಮೂರು ಅಥವಾ ಹೆಚ್ಚು ರೇಖಾಖಂಡಗಳು ಅವುಗಳ ಅಂತ್ಯ ಬಿಂದುಗಳಲ್ಲಿ ಸಂಧಿಸಿದಾಗ, ಅವುಗಳಿಂದ ಸುತ್ತುವರಿದ ಆಕೃತಿಯನ್ನು ಬಹುಭುಜಾಕೃತಿ (Polygons) ಎನ್ನುವರು. ರೇಖಾಖಂಡಗಳು ಸಂಧಿಸುವ ಅಂತ್ಯ ಬಿಂದುಗಳನ್ನು ಬಹುಭುಜದ ಶೃಂಗ (vertices) ಎನ್ನುವರು. ಬಹುಭುಜಾಕೃತಿಯನ್ನುಂಟು ಮಾಡುವ ರೇಖಾಖಂಡಗಳನ್ನು ಆ ಬಹುಭುಜದ ಬಾಹು(ಭುಜ) (sides) ಎನ್ನುವರು.
|
ಒಂದು ಬಹುಭುಜಾಕೃತಿಯಲ್ಲಿ ಅನುಕ್ರಮವಲ್ಲದ ಯಾವುದೇ ಎರಡು ಶೃಂಗಬಿಂದುಗಳನ್ನು ಸೇರಿಸುವ ರೇಖಾಖಂಡವನ್ನು ಆ ಬಹುಭುಜದ ಕರ್ಣ (diagonal) ಎನ್ನುವರು. ಪಕ್ಕದ ಚಿತ್ರದಲ್ಲಿ(ಪಂಚಭುಜ): |
|
|||||||
|
||||||||
|
ಗಮನಿಸಿ: ಒಂದು ಬಹುಭುಜಾಕೃತಿಯಲ್ಲಿ ಬಾಹುಗಳ ಸಂಖ್ಯೆ = ಕೋನಗಳ ಸಂಖ್ಯೆ = ಶೃಂಗಬಿಂದುಗಳ ಸಂಖ್ಯೆ |
||||||||
|
ತ್ರಿಭುಜ, ಚತುರ್ಭುಜ, ಪಂಚಭುಜ, ಷಡ್ಭುಜ, ಸಪ್ತಭುಜ, ಅಷ್ಟಭುಜ …..ಇತ್ಯಾದಿ ಇವೆಲ್ಲವೂ ಬಹುಭುಜಾಕೃತಿಗಳಿಗೆ ಉದಾಹರಣೆಗಳು. |
ವ್ಯಾಖ್ಯೆ:
1. ಒಂದು ಬಹುಭುಜಾಕೃತಿಯಲ್ಲಿ
ಅದರ ಬಾಹುಗಳೆಲ್ಲವೂ ಸಮವಾಗಿದ್ದು
ಕೋನಗಳೆಲ್ಲವೂ ಸಮವಾಗಿದ್ದರೆ, ಅದನ್ನು ನಿಯಮಿತ ಬಹುಭುಜಾಕೃತಿ (regular polygon) ಎನ್ನುವರು. (ಉದಾ:
ಚೌಕ(ವರ್ಗ)
2. ಒಂದು ಬಹುಭುಜಾಕೃತಿಯ ಒಳವಲಯ (interior region) ಅಥವಾ ಕ್ಷೇತ್ರವೂ,
ರೇಖೆಗಳಿಂದ ಆವೃತಗೊಂಡಿರುವ ಸಮತಲದಲ್ಲಿನ ಒಂದು ಭಾಗವಾಗಿದೆ.
ಅಭ್ಯಾಸ:
1. ಒಂದು ನಿಯಮಿತ ಪಂಚಭುಜವನ್ನು ರಚಿಸಿ. ಇದರ ಎಲ್ಲಾ ಒಳಕೋನಗಳು 1080 ಆಗಿರುವುದನ್ನು ಗಮನಿಸಿ.
2. ಒಂದು ನಿಯಮಿತ ಷಡ್ಭುಜವನ್ನ ರಚಿಸಿ. ಇದರ ಎಲ್ಲಾ ಒಳಕೋನಗಳು 1200 ಆಗಿರುವುದನ್ನು ಗಮನಿಸಿ.
ಒಂದು ನಿಯಮಿತ ಬಹುಭುಜದ ಎಲ್ಲಾ ಶೃಂಗಬಿಂದುಗಳು ಒಂದೇ ವೃತ್ತದ ಪರಿಧಿಯ ಮೇಲಿದ್ದರೆ, ಅಥವಾ ನಿಯಮಿತ ಬಹುಭುಜದ ಎಲ್ಲಾ ಬಾಹುಗಳು ಒಂದೇ ವೃತ್ತದ ಜ್ಯಾಗಳಾಗಿದ್ದರೆ,ಅಂತಹ ಬಹುಭುಜಾಕೃತಿಯನ್ನು “ಅಂತಸ್ಥನಿಯಮಿತ ಬಹುಭುಜಾಕೃತಿ” (inscribed regular polygon) ಎನ್ನುತ್ತೇವೆ.
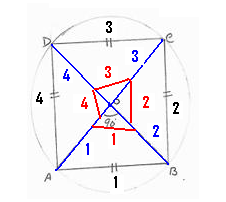
ಒಂದು ನಿಯಮಿತ ಅಂತಸ್ಥ ಬಹುಭುಜದ(ಚಿತ್ರದಲ್ಲಿ ಚತುರ್ಭುಜ)ಎಲ್ಲಾ ಶೃಂಗ ಬಿಂದುಗಳನ್ನು ವೃತ್ತ ಕೇಂದ್ರಕ್ಕೆ ಜೋಡಿಸಿ.
ಆಗ ನೀವು ಈ ಕೆಳಗಿನ ಅಂಶಗಳನ್ನು ಗಮನಿಸುತ್ತೀರಿ:-
|
1. ಶೃಂಗ ಬಿಂದುಗಳನ್ನು (A, B,C,D) ಕೇಂದ್ರಕ್ಕೆ (0) ಜೋಡಿಸುವ ಸರಳರೇಖೆಗಳ ಸಂಖ್ಯೆಯು ಬಹುಭುಜದ ಬಾಹುಗಳ ಸಂಖ್ಯೆಗೆ ಸಮ(ಚಿತ್ರದಲ್ಲಿ 4 : AO,
BO,CO,DO ) 2. ವೃತ್ತ ಕೇಂದ್ರದಲ್ಲಿ ಉಂಟಾದ ಕೋನಗಳ ಸಂಖ್ಯೆಯು ಬಹುಭುಜದ ಬಾಹುಗಳ ಸಂಖ್ಯೆಗೆ ಸಮ (ಚಿತ್ರದಲ್ಲಿ 4: 3. ವೃತ್ತ ಕೇಂದ್ರದಲ್ಲಿ ಉಂಟಾದ ಎಲ್ಲಾ ಕೋನಗಳು ಪರಸ್ಪರ ಸಮ (900) |
|
6.6 ಉದಾ 1: 4 ಸೆಂ.ಮಿ. ತ್ರಿಜ್ಯವಿರುವ ಒಂದು ವೃತ್ತದಲ್ಲಿ ಒಂದು ಅಂತಸ್ಥ ನಿಯಮಿತ ಚತುರ್ಭುಜ (ವರ್ಗ)ವನ್ನು ರಚಿಸಿ:-
|
ಹಂತ 1: ಕೇಂದ್ರದಲ್ಲಿ ಉಂಟಾಗುವ ಕೋನ (ಕೇಂದ್ರೀಯ ಕೋನ)ವನ್ನು ಲೆಕ್ಕಹಾಕಲು 3600 ಯನ್ನು ನಿಯಮಿತ ಚತುರ್ಭುಜದ ಬಾಹುಗಳ ಸಂಖ್ಯೆ (=4) ಯಿಂದ ಭಾಗಿಸಿ. ಕೇಂದ್ರೀಯ ಕೋನ = 360/4 = 900 ಹಂತ 2: O ಬಿಂದುವನ್ನು ಕೇಂದ್ರವಾಗಿಟ್ಟುಕೊಂಡು 4 ಸೆಂ.ಮಿ. ತ್ರಿಜ್ಯದಿಂದ ಒಂದು ವೃತ್ತವನ್ನೆಳೆಯಿರಿ. ಹಂತ 3: ‘O’ ದಿಂದ ಎರಡು ರೇಖೆಗಳು OA
ಮತ್ತು OBಗಳನ್ನು (ಈ ಕೋನದ ಅಳತೆ ಹಂತ 1 ರಲ್ಲಿ ಪಡೆದದ್ದು). ಹಂತ 4: Bಯನ್ನ ಕೇಂದ್ರವಾಗಿಟ್ಟುಕೊಂಡುAB ತ್ರಿಜ್ಯದಿಂದ ವೃತ್ತ ಪರಿಧಿಯನ್ನು C ಯಲ್ಲಿ ಕಡಿಯುವಂತೆ ಒಂದು ಕಂಸವನ್ನೆಳೆಯಿರಿ. ಹಂತ 5: C ಯನ್ನ ಕೇಂದ್ರವಾಗಿಟ್ಟುಕೊಂಡು ಅದೇ ತ್ರಿಜ್ಯದಿಂದ, ವೃತ್ತ ಪರಿಧಿಯನ್ನ D ಯಲ್ಲಿ ಕಡಿಯುವಂತೆ ಒಂದು ಕಂಸವನ್ನೆಳೆಯಿರಿ. ಹಂತ 6: A, B, C ಮತ್ತು D ಬಿಂದುಗಳನ್ನು ಜೋಡಿಸಿ, ABCD ಚತುರ್ಭುಜವನ್ನು ಪಡೆಯಿರಿ. |
|
ದತ್ತ ತ್ರಿಜ್ಯದ ವೃತ್ತದಲ್ಲಿ ಅಂತಸ್ಥ ನಿಯಮಿತ ಬಹುಭುಜವನ್ನು ರಚಿಸುವ ಸಾಮಾನ್ಯಕ್ರಮ.
|
ಹಂತ 1: ಕೇಂದ್ರದಲ್ಲಿ ಉಂಟಾಗುವ ಕೋನವನ್ನು ಲೆಕ್ಕಮಾಡಲು 3600 ಯನ್ನು ನಿಯಮಿತ ಬಹುಭುಜದ ಬಾಹುಗಳ ಸಂಖ್ಯೆಯಿಂದ ಭಾಗಿಸಿ. ಕೇಂದ್ರದಲ್ಲಿ ಉಂಟಾಗುವ ಕೋನ (x) = 360÷(n : ಬಹುಭುಜದ ಬಾಹುಗಳ ಸಂಖ್ಯೆ) ಹಂತ 2: O ಬಿಂದುವನ್ನು ಕೇಂದ್ರವಾಗಿಟ್ಟುಕೊಂಡು ದತ್ತ ತ್ರಿಜ್ಯದಿಂದ ಒಂದು ವೃತ್ತವನ್ನು ರಚಿಸಿ ಹಂತ 3: ಕೇಂದ್ರ ‘O’ ದಿಂದ ಹಂತ 1 ರಲ್ಲಿ ಪಡೆದ ಕೋನ ಉಂಟಾಗುವಂತೆ, OA ಮತ್ತು ಹಂತ 4: B ಯನ್ನು ಕೇಂದ್ರವಾಗಿಟ್ಟುಕೊಂಡು AB ತ್ರಿಜ್ಯದಿಂದ C ಯಲ್ಲಿ ಕಡಿಯುವಂತೆ ಒಂದು ಕಂಸವನ್ನೆಳೆಯಿರಿ. ಹಂತ 5: C ಯನ್ನ ಕೇಂದ್ರವಾಗಿಟ್ಟುಕೊಂಡು ಅದೇ ತ್ರಿಜ್ಯದಿಂದ, ವೃತ್ತ ಪರಿಧಿಯನ್ನ D ಯಲ್ಲಿ ಕಡಿಯುವಂತೆ ಒಂದು ಕಂಸವನ್ನೆಳೆಯಿರಿ. ಹಂತ 6: ಹಂತ 5 ರಲ್ಲಿ ಮಾಡಿದ ರಚನೆಯನ್ನು ಮುಂದುವರಿಸಿದರೆ, ಕೊನೆಯ ಕಂಸ A ಯಲ್ಲಿ ಕಡಿಯುತ್ತದೆ. ಹಂತ 7: ವೃತ್ತ ಪಂಧಿಯ ಮೇಲಿನ ಈ ಎಲ್ಲಾ ಬಿಂದುಗಳನ್ನು ಜೋಡಿಸಿ, ಬೇಕಾದ ಬಹುಭುಜವನ್ನು ಪಡೆಯಿರಿ. |
|
ಗಮನಿಸಿ: ವಿವಿಧ ಅಂತಸ್ಥ ನಿಯಮಿತ ಬಹುಭುಜಗಳ ಕೇಂದ್ರದಲ್ಲಿ
ಉಂಟಾಗುವ ಕೋನಗಳು:-
|
ಬಹುಭುಜದ ವಿಧ |
ಬಾಹುಗಳ ಸಂಖ್ಯೆ (n ) |
ಕೇಂದ್ರದಲ್ಲಿ ಆಗುವ ಕೋನ =(x) |
|
ತ್ರಿಭುಜ |
3 |
1200(360÷3) |
|
ಚತುರ್ಭುಜ |
4 |
900(360÷4) |
|
ಪಂಚಭುಜ |
5 |
720(360÷5) |
|
ಷಡ್ಭುಜ |
6 |
600(360÷6) |
|
ಅಷ್ಟಭುಜ |
8 |
450(360÷8) |
|
ನವಭುಜ |
9 |
400(360÷9) |
|
ದಶಭುಜ |
10 |
360(360÷10) |
7 ಬಾಹುಗಳುಳ್ಳ ಬಹುಭುಜವನ್ನ ಮೇಲಿನ ತಃಖ್ತೆಯಲ್ಲಿ ಏಕೆ ಬರೆದಿಲ್ಲವೆಂದು ಆಲೋಚಿಸಿ.
6.6.1 ಪ್ರಮೇಯ 1: ‘n’ ಬಾಹುಗಳುಳ್ಳ ಬಹುಭುಜಾಕೃತಿಯ ಒಳಕೋನಗಳ ಮೊತ್ತ (2n-4) ಲಂಬಕೋನಗಳಾಗಿರುತ್ತವೆ.
ದತ್ತ: ABCDEFG…ಯು n ಬಾಹುಗಳುಳ್ಳ ಬಹುಭುಜಾಕೃತಿ.
ಸಾಧನೀಯ:
ಒಳಕೋನಗಳ ಮೊತ್ತ = (2n-4) ಲಂಬಕೋನಗಳು.
ರಚನೆ: ಬಹುಭುಜಾಕೃತಿಯ ಒಳಗಿನ ಯಾವುದೇ ಬಿಂದು O ವಿನಿಂದ ಪ್ರತೀ ಶೃಂಗಕ್ಕೆ(A,B,C…) ಸರಳರೇಖೆಯನ್ನು
ಎಳೆಯಿರಿ.
|
ಹಂತ |
ಹೇಳಿಕೆ |
ಕಾರಣ |
|
|
1 |
ಬಹುಭುಜಾಕೃತಿಯು n ಸಂಖ್ಯೆಯ
ತ್ರಿಕೋನಗಳನ್ನು ಹೊಂದಿದೆ. |
ಬಹುಭುಜಾಕೃತಿಯಲ್ಲಿ n ಬಾಹುಗಳಿವೆ |
|
|
2 |
ಎಲ್ಲಾ ತ್ರಿಕೋನಗಳ ಕೋನಗಳ ಮೊತ್ತ = n*2 ಲಂಬಕೋನಗಳು |
ತ್ರಿಕೋನದ ಕೋನಗಳ ಮೊತ್ತ = 2 ಲಂಬಕೋನಗಳು |
|
|
3 |
O ನಲ್ಲಿನ ಎಲ್ಲಾ ಕೋನಗಳ ಮೊತ್ತ
= 4 ಲಂಬಕೋನಗಳು |
ಕೇಂದ್ರದಲ್ಲಿನ ಕೋನ = 3600 |
|
|
4 |
n ತ್ರಿಕೋನಗಳ ಎಲ್ಲಾ ಕೋನಗಳ ಮೊತ್ತ = ಬಹುಭುಜಾಕೃತಿಯ ಒಳಕೋನಗಳ ಮೊತ್ತ + O ನಲ್ಲಿನ ಕೋನ |
ರಚನೆ |
|
|
5 |
ಬಹುಭುಜಾಕೃತಿಯ ಒಳಕೋನಗಳ ಮೊತ್ತ = n ತ್ರಿಕೋನಗಳ ಎಲ್ಲಾ ಕೋನಗಳ ಮೊತ್ತ – O ನಲ್ಲಿನ ಕೋನ |
ಹಂತ 4 ರ
ಪಕ್ಷಾಂತರ |
|
|
6 |
= 2n ಲಂಬಕೋನಗಳು - 4 ಲಂಬಕೋನಗಳು = (2n-4) ಲಂಬಕೋನಗಳು |
ಹಂತ 2 ಮತ್ತು 3 ರ ಆದೇಶ |
6.6.1 ಉಪಪ್ರಮೇಯ: ಬಹುಭುಜಾಕೃತಿಯಲ್ಲಿನ ಎಲ್ಲಾ
ಬಾಹುಗಳನ್ನು ನಿಯಮಿತವಾಗಿ ಒಂದೇ ಕಡೆಗೆ ವೃದ್ಧಿಸಿದಾಗ ಅಲ್ಲಿ ಉಂಟಾಗುವ ಹೊರಕೋನಗಳ ಮೊತ್ತವು ನಾಲ್ಕು
ಲಂಬಕೋನಗಳಿಗೆ ಸಮನಾಗಿರುತ್ತದೆ. ( a,b,c…ಗಳು ಹೊರಕೋನಗಳು.)
|
ಹಂತ |
ಹೇಳಿಕೆ |
ಕಾರಣ |
|
|
1 |
ಒಂದು ಶೃಂಗದಲ್ಲಿನ ಒಳ ಮತ್ತು
ಹೊರಕೋನ ಗಳ ಮೊತ್ತ =2 ಲಂಬಕೋನಗಳು |
ಸರಳರೇಖೆಯ ಮೇಲಿನ ಕೋನ = 2 ಲಂಬಕೋನಗಳು |
|
|
2 |
n ಶೃಂಗಳಲ್ಲಿನ ಒಳ ಮತ್ತು
ಹೊರಕೋನ ಗಳ ಮೊತ್ತ =2n ಲಂಬಕೋನಗಳು |
ಹಂತ 1 |
|
|
3 |
ಬಹುಭುಜದ ಒಳಕೋನ ಗಳ
ಮೊತ್ತ + ಹೊರಕೋನ ಗಳ ಮೊತ್ತ = n ಶೃಂಗಗಳಲ್ಲಿನ
ಒಳಕೋನ ಮತ್ತು ಹೊರಕೋನಗಳ ಮೊತ್ತ |
ರಚನೆ |
|
|
4 |
ಹೊರಕೋನ ಗಳ ಮೊತ್ತ =n ಶೃಂಗಗಳಲ್ಲಿನ
ಒಳಕೋನ ಮತ್ತು ಹೊರಕೋನಗಳ ಮೊತ್ತ - ಒಳಕೋನ ಗಳ ಮೊತ್ತ |
ಹಂತ 3 ರ
ಪಕ್ಷಾಂತರ |
|
|
5 |
= 2n ಲಂಬಕೋನಗಳು – (2n-4) ಲಂಬಕೋನಗಳು |
( ಹಂತ 2 ಮತ್ತು 6.6.1 ಪ್ರಮೇಯ) |
|
|
6 |
= 4 ಲಂಬಕೋನಗಳು |
|
ಗಮನಿಸಿ:
|
ಸಂ |
ಲಕ್ಷಣಗಳು |
|
1 |
ನಿಯಮಿತ ಬಹುಭುಜದ ಪ್ರತಿಯೊಂದು ಒಳ ಕೋನ = (2n-4)*90/n |
|
2 |
ನಿಯಮಿತ ಬಹುಭುಜದ ಪ್ರತಿಯೊಂದು ಹೊರ ಕೋನ (x) = 4*90/n =
360/n |
|
3 |
ನಿಯಮಿತ ಬಹುಭುಜದ ಹೊರಕೋನ x ಆದರೆ, ಅದರ ಬಾಹುಗಳ ಸಂಖ್ಯೆ (n) = 360/x |
6.6.1 ಸಮಸ್ಯೆ 1: AB, BC ಮತ್ತು CD ಗಳು ನಿಯಮಿತ ಬಹುಭುಜದ ಅನುಕ್ರಮ ಬಾಹುಗಳು ಮತ್ತು ![]() BAC = 150 ಆದರೆ
BAC = 150 ಆದರೆ
(i) ಬಹುಭುಜದ ಪ್ರತೀ ಹೊರಕೋನ ಎಷ್ಟು?
(ii) ಬಹುಭುಜದ ಪ್ರತೀ ಒಳಕೋನ ಎಷ್ಟು?
(iii) ಬಹುಭುಜದಲ್ಲಿ ಎಷ್ಟು ಬಾಹುಗಳಿವೆ?
ಪರಿಹಾರ:
|
AB=BC ಆಗಿರುವುದರಿಂದ ABC ಯು ಸಮದ್ವಿಬಾಹು ತ್ರಿಭುಜವಾಗಿದೆ. ಹಾಗಾಗಿ ಪ್ರತೀ ಒಳಕೋನ = 1500 ಪ್ರತೀ ಹೊರಕೋನ = 300 ಬಹುಭುಜದಲ್ಲಿನ ಬಾಹುಗಳು = 360/30 = 12 |
|
6.6.1 ಸಮಸ್ಯೆ 2: (n-1)
ಬಾಹುಗಳಿರುವ ನಿಯಮಿತ ಬಹುಭುಜದ ಹೊರಕೋನ ಮತ್ತು (n+1) ಬಾಹುಗಳಿರುವ ನಿಯಮಿತ ಬಹುಭುಜದ ಹೊರಕೋನಗಳ ವ್ಯತ್ಯಾಸ 90 ಆದರೆ n ಎಷ್ಟು
ಅವುಗಳ ವ್ಯತ್ಯಾಸ ಅಂದರೆ
ಪರಿಹಾರ:
1. (n-1) ಬಾಹುಗಳಿರುವ ನಿಯಮಿತ ಬಹುಭುಜದ ಹೊರಕೋನ =
360/(n-1)
2. (n+1) ಬಾಹುಗಳಿರುವ ನಿಯಮಿತ ಬಹುಭುಜದ ಹೊರಕೋನ = 360/(n+1)
ಅವುಗಳ ವ್ಯತ್ಯಾಸ = 9
![]() 360/(n-1)
– 360/(n+1) = 9
360/(n-1)
– 360/(n+1) = 9
i.e. {360(n+1) - 360(n-1)}/{(n+1)(n-1)}
= 9
i.e. 720/n2-1 = 9
i.e. n2-1 = 80
i.e. n2 = 81
i.e. n = 9
ನಿಯಮಿತ ಬಹುಭುಜದಲ್ಲಿ 9 ಬಾಹುಗಳಿವೆ.
6.6 ಕಲಿತ ಸಾರಾಂಶ
|
ಸಂ. |
ಕಲಿತ ಮುಖ್ಯಾಂಶಗಳು |
|
1 |
ಒಂದೇ ಸಮತಲದಲ್ಲಿರುವ, ಏಕರೇಖಾಗತವಲ್ಲದ ಮೂರು ಅಥವಾ ಹೆಚ್ಚು ರೇಖಾಖಂಡಗಳು ಅವುಗಳ ಅಂತ್ಯ ಬಿಂದುಗಳಲ್ಲಿ ಸಂಧಿಸಿದಾಗ, ಅವುಗಳಿಂದ ಸುತ್ತುವರಿದ ಆಕೃತಿಯೇ ಬಹುಭುಜ. |
|
2 |
ಸಮಕೋನೀಯವಾಗಿದ್ದು ಸಮವಾದ ಬಾಹುಗಳನ್ನು ಹೊಂದಿರುವ ಬಹುಭುಜವೇ ನಿಯಮಿತ ಬಹುಭುಜ. |
|
3 |
ಒಂದು ನಿಯಮಿತ ಬಹುಭುಜದ ಶೃಂಗ ಬಿಂದುಗಳು ಒಂದು ವೃತ್ತದ ಪಂಧಿಯ ಮೇಲಿದ್ದರೆ, ಅದು ಅಂತಸ್ಥ ನಿಯಮಿತ ಬಹುಭುಜ. |