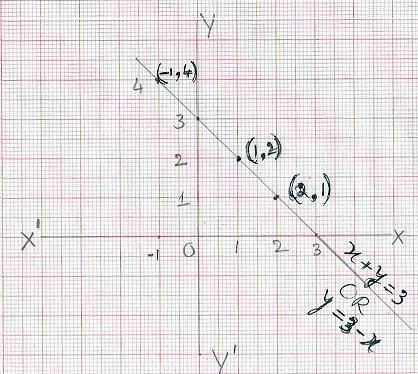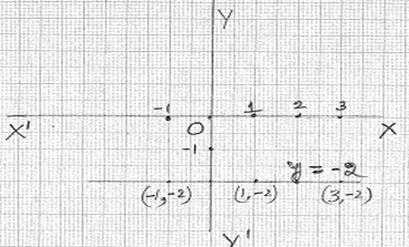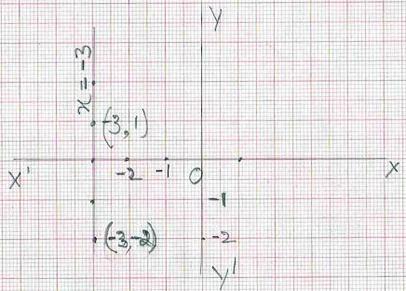7.1 Rectangular Co–ordinates and Graphs:

 

Introduction :   we have learnt how numbers can be represented on a number line ( it is denoted by a point which is no dimension).Line had one dimension. Can we locate our house as a point on a line?  Don’t we need to have longitude and latitude to locate a city on a world map?

Similarly, we need to provide the row and column position (Main and cross) to locate a house in a street? This representation can be called as two dimensional representations. This branch of mathematics is called co-ordinate geometry.

 

The word graph means ‘to paint or ‘to draw’.

 

By convention we write positive numbers on right side of zero and negative numbers

on the left side of zero on a number line(Refer lesson 1.1)

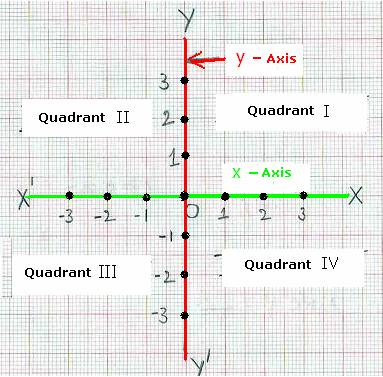
In the graph sheet, the horizontal line is conventionally called ‘x axis’.

Thus, the line OX   represents positive numbers and the line OX1 (X1 is also called –x)

represents negative numbers

Let us draw a perpendicular line at O to x axis and extend this line both above and below the x axis. Again, by convention we call this vertical line as ‘y axis’.

By convention line OY represents positive numbers and the line OY1(Y1 is also called –y)

represents negative numbers.

 

The x axis and y axis together are called ‘coordinate axes’

 

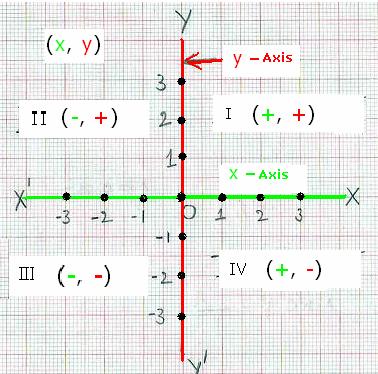
The coordinate axes divide the plane into 4 parts which we call as the ‘quadrants’   

named as Quadrant I, Quadrant II, Quadrant III, Quadrant IV in the anti clock wise

direction. On the graph sheet we note markings on both x axis and y axis at

equal distances (1cm) both to the left of O and right of O on x axis, as well as above O

and below O on y axis  at equal distances with same unit of measurement (say 1cm).

 

 

1. On OX it will be to the right of O at 1cm, 2cm, 3cm .,.

2. On OX1 to the left of O at -1cm, -2cm, -3cm …..

3. On OY above O at 1cm, 2cm, 3cm, ….

4. On OY1 below O at -1cm, -2cm, -3cm …

 

 

Plotting of points on a graph sheet:

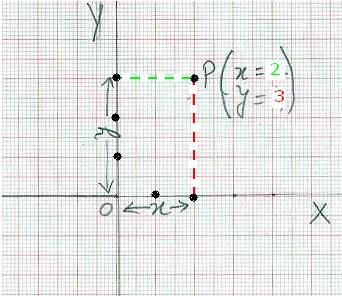
On I Quadrant, mark a point P (anywhere you like, above x axis and to the right of y axis). From P draw lines parallel to both x axis and y axis. These lines have to meet X axis and Y

axis some where forming a rectangle.

 

The distance from O to the point where the perpendicular line from P meets x axis

is called ‘x- coordinate’ or ‘abscissa’ of point P.

 

The distance from O to the point where the horizontal line from P meets y axis is

 called ‘y- coordinate’ or ‘ordinate ’

of point P.

 

In the adjoining graph x-coordinate for P is 2 units( cms) and y-coordinate for P

is 4 units(cms) and P can be represented as P(2,4),  these coordinates are also

called ‘rectangular coordinates’ (because the closed figure is a rectangle)

 

 

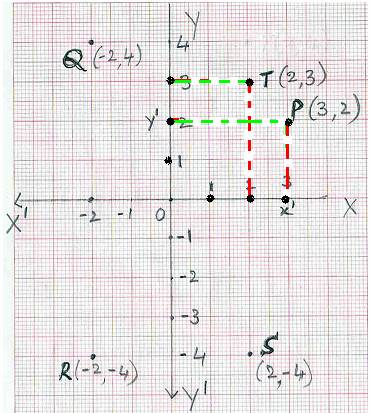
7.1 Problem 1: Plot the point P(3, 2) on the plane.

 

Solution:

Step 1: On a graph sheet mark(x1) on x axis at 3cm to the right of O

Step 2: On the same sheet mark (y1) on y axis at 2cm above O

Step 3: Construct a rectangle with sides Ox1 and Oy1   in Quadrant I.

The point where lines parallel to Ox1 and OY   meet is P (3, 2)

 

Exercise: Plot the point T(2, 3) on the plane.

 

Do you notice that points P (3, 2), T (2, 3) are not one and the same?

 

Since no two points have same coordinates x and y, the coordinate (x, y) is

called ‘ordered pair’.

 

Exercise:  Mark points Q(-2, 4),  R(-2, -4), S(2, -4) on the plane.

 

By convention note that

1.  Negative x coordinate is marked to the left of O on x axis (i.e. on line X1O)

2.  Negative y coordinate is marked below the x axis (i.e. on line OY1)

 

We notice that:

1. Point Q (-2, 4) is in Quadrant II

2. Point R (-2, -4) is in Quadrant III

3. Point S (2, -4) is in   Quadrant IV

 

Observations:

1. The coordinates of the origin O is (0, 0).

2. The coordinates of any point on x axis is (x, 0).

3. The coordinates of any point on y axis is (0, y).

 

       

 

 

Quadrant

x-coordinate

y-coordinate

Point(x,y)

1

I

+

+

(+, +)

2

II

-

+

(-, +)

3

III

-

-

(-, -)

4

IV

+

-

(+, -)

 

7.1.1 Drawing graph for a linear equation:

 

We know that linear equation is an equation involving only linear polynomial or variable in first degree.

 

Let us consider the below mentioned relations. In these relations let the other number be x and the first number be y

 

No.

Relationship

Equivalent equation

1

A number is equal to other number

y = x

2

A number is twice the other number

y = 2x

3

A number is  one more than twice the other number

y = 2x+1

4

A number is twice (the sum of other number increased by 2)

y = 2(x+2)

5

Difference between the other number and the number is 3

x-y  =3 or  –y = 3-x(transposition) or y  = x-3(multiply by -1)

6

Sum of number and other number is 3

x+y= 3  or y  = 3-x(transposition)

 

All the above equations are of first degree and are of general form y = mx + c where c is a constant. Even if the given equation is of the form ax+by+c = 0 it can always be converted to the form y =mx+c. How ?

 

1

ax+by+c = 0

Given.  

2

by= -ax-c

Transposition(subtract both sides by ax+c)

3

y= (-a/b)x-(c/b)

Divide both sides by b

4

y =mx+z

m= -(a/b), z= -(c/b)

 

7.1.1 Problem 1: Draw the graph for the  equation x+y =3

 

Solution:

Step 1 : Convert the given  equation to  the form of  y = (i.e. LHS will have only y).

So we have y = 3-x(transposition).

Step 2 : For few values of x (though 2 is enough) get  values of y and record them in a table like:

            

x à

0

-1

1

2

y à

3

4

2

1

(x,y)

(0,3)

(-1,4)

(1,2)

(2,1)

 

Step 3 :  Plot the points represented by (x,y) coordinates  on a graph sheet and join them to get a straight line This line represents the equation x+y =3(or y= -x +3)

 

Verification: How are we sure that this line represents the equation x+y=3?

 

For x=0.5 find out the y-coordinate of the point on this straight line. We notice that it is 2.5 and thus the point (0.5, 2.5) is on the line

Substituting this value in the given equation we notice that x+y =0.5+2.5 = 3. So any point on the straight line we have just drawn, satisfies the given linear equation.

Similarly we find that point (3,0) is a point on the drawn straight line and satisfies the given equation. This proves that the graph represents the given equation.

 

Since y= mx+c is a first degree equation and its graph represents a straight line, we call first degree equations as linear equations.

Note :

1. Though only two points are enough to draw a straight line we have prepared more values of (x,y) to indicate that there are many solutions to x+y=3

2. It is also clear from the graph that many coordinates ( x, y) on the  line x+y =3 {for example (4,-1)}satisfy the given equation x+y=3

 

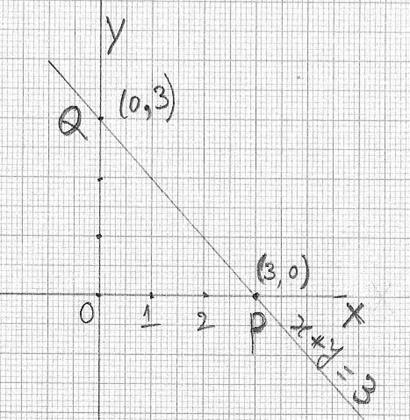
Alternate Method of drawing  graph:

We know that to draw a straight line we need only 2 points.

Hence why is it necessary to have tables of (x, y) for various values of x and y?

Why not  have just 2 points with one point on x axis and another point on y axis, so that by joining these two points we can draw a straight line?

A point on x axis will always have its y coordinate as 0. Similarly a point on y axis will always have  its x coordinate as 0

 

Definition:

1. ‘x- intercept’  of a linear equation is the x-coordinate of the point where graph crosses the x –axis( It is the distance of point from O on x-axis).

It’s coordinate has to be (x,0). To get this value of x, substitute y=0 in the given equation.

 

2.  ‘y- intercept’  of a linear equation is the y-coordinate of the point where graph crosses the y –axis( It is the distance of point from O on y-axis).

It’s coordinate has to be (0, y).To get this value of y, substitute x=0 in the given equation.

 

Note that intercept means cut and hence x intercept means point of cutting of x axis and y intercept means point of cutting of y axis.

 

Let us plot the graph using this alternate method for the equation x+y = 3(Problem 7.1.1.1)

By substituting y=0 in the above equation we get x=3. Thus P(3,0) is the x-intercept

By substituting x=0 in the above equation we get y=3. Thus Q(0,3) is the y-intercept

By joining P and Q we get the graph for the line x+y =3.This is the same graph we have drawn in Problem 7.1.1.1

 

7.1.1 Problem 2: Draw a graph for y = -2

 

Solution:

Step 1 :  The equation can be interpreted  as ‘for any value of x, y is always -2’ and  hence can be  represented as y =0x-2

Step 2: For few values of x (though 2 is enough) find  values of y and record them in a table like:

           

x à

-1

1

3

y à

-2

-2

-2

(x,y)

(-1,-2)

(1,-2)

(3,-2)

 

Step 3 :  Plot the points represented by (x, y) coordinates  on a graph sheet and join them to get a straight line. This line represents the equation y=-2.

You can verify that the point (2,-2) is on this drawn line also satisfies the equation y = -2.

Note that this drawn line is parallel to x axis

 

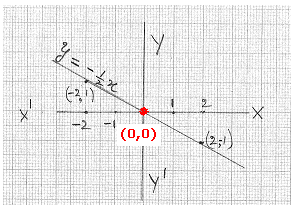
7.1.1 Problem 3: Draw a graph for 2y = -x.

This is of the form y=mx

 

Solution:

Step 1:  Convert the given equation to the form of y = (i.e. LHS will  only have y) so y = - (1/2)x

Step 2: For 2 values of x find values of y and record them in a table as shown below

   

x à

-2

2

0

y à

1

-1

0

(x, y)

(-2,1)

(2,-1)

(0,0)

 

Step 3:  Plot the points represented by (x, y) coordinates on a graph sheet and join them to get a straight line. This line represents the equation y= -(1/2)x

You can verify that the point (1,-1/2) is on this drawn line and also satisfies the equation y = -2.

Note this drawn line passes through origin (0, 0). Thus if y=mx, then the line passes through origin.

 

7.1.1 Problem 4: Draw a graph for x = -3. The equation can be interpreted as ‘for any value of y, x is always -3’ or x+3=0

 

Solution:

Step1: Since the equation does not have y term, we can say 0y = -x-3

 

x à

-3

-3

-3

y à

1

-1

-2

(x,y)

(-3,1)

(-3,-1)

(-3,-2)

 

 

Step 2:  Plot the points represented by (x, y) coordinates on a graph sheet and

join them to get a straight line. This line represents the equation x=-3

Note that this drawn line is parallel to y axis.

 

 

7.1 Summary of learning

 

 

No

Points to remember

1

x axis and y axis are called co ordinate axis

2

Any point  is represented by a ordered pair(x, y) called coordinates of that point

3

Origin’s co ordinates are (0,0)

4

Any point on the x axis has (x,0) as its coordinate and

any point on the y axis has(0,y) as its coordinate

5

The equation to a line is of the form y = mx+c(which is of first degree) and is called linear graph

6

The graph x = constant is a line parallel to y axis and

the graph y =  constant is a line parallel to  x axis

7

The graph y = mx  is a line which passes through Origin

8

x- intercept  of a linear equation is the x-coordinate of the point

where the line  crosses the x –axis at (x,0)

9

y- intercept  of a linear equation is the y-coordinate of the point

where the line  crosses the y –axis at (0,y)