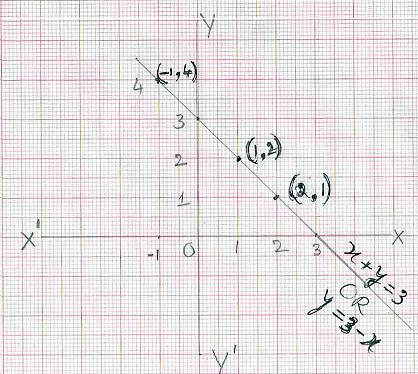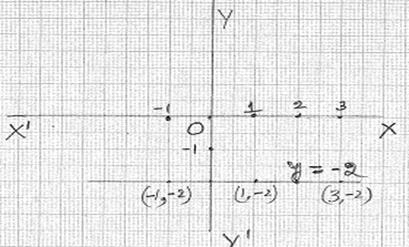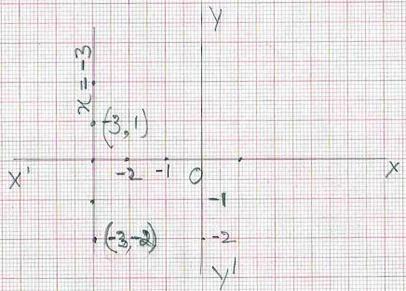7.1 ಆಯತ ನಿರ್ದೇಶಾಂಕಗಳ ಚತುರ್ಥಕಗಳು ಮತ್ತು
ನಕ್ಷೆಗಳು (Rectangular Co–ordinates and
Graphs):
ನಾವೀಗಾಗಲೇ ಸಂಖ್ಯಾರೇಖೆಯನ್ನು ಎಳೆಯಲು ಮತ್ತು ಸಂಖ್ಯಾರೇಖೆಯ ಮೇಲೆ ಸಂಖ್ಯೆಗಳನ್ನು ಬಿಂದುಗಳಾಗಿ ಗುರುತಿಸುವುದನ್ನು ಕಲಿತಿದ್ದೇವೆ.
ಬಿಂದುವಿಗೆ ಯಾವುದೇ ಮಟ್ಟ(ಆಯಾಮ,ಅಳತೆ) ಇಲ್ಲ. ಅದರೆ ಅದೇ ಸರಳ ರೇಖೆಗೆ ಒಂದು ಮಟ್ಟ(ಉದ್ದ) ಇದೆ. ಹಾಗೆಯೇ ಕ್ಷೇತ್ರ ಫಲ ಇರುವ ತ್ರಿಭುಜ, ಚತುರ್ಭುಜ ಆಕೃತಿಗಳಿಗೆ ಎರಡು ಮಟ್ಟಗಳು ಇವೆ. ಗಾತ್ರ ಅಥವಾ ಘನ ಫಲ ಇರುವ ಗೋಳ, ಸಿಲಿಂಡರ್ ಇವುಗಳಿಗೆ ಮೂರು ಮಟ್ಟಗಳು ಇವೆ.
ನಮ್ಮ ಮನೆಗಳನ್ನು ಕಾಗದದ ಮೇಲೆ ಮತ್ತು ಒಂದು ನಗರವನ್ನು ಒಂದು ಭೂಪಟದ ಮೇಲೆ ಒಂದು ಬಿಂದುವಿನಿಂದ ಗುರುತಿಸಲು ಸಾಧ್ಯವೇ?
ನಮ್ಮ ನಗರಗಳನ್ನು ಭೂಪಟದಲ್ಲಿ ಗುರುತಿಸಲು ಅಕ್ಷಾಂಶ ಮತ್ತು ರೇಖಾಂಶಗಳು ಬೇಕು. ಅದೇ ರೀತಿ ಮನೆಯನ್ನು ಗುರುತಿಸಲು ಎರಡು ಮಟ್ಟಗಳು ಬೇಕು.
ಗಣಿತದ ಈ ವಿಭಾಗದ ಕಲಿಕೆಯೇ ನಕ್ಷೆ. ನಕ್ಷೆ ಎಂದರೆ ‘ಬರೆಯುವುದು’ ಅಥವಾ ‘ಗುರುತಿಸುವುದು’ ಅಥವಾ ‘ಎಳೆಯುವುದು’
(‘to
paint or ‘to draw’).
ನಾವು ರೂಢಿಯಲ್ಲಿ, ಸಂಖ್ಯಾರೇಖೆಯ ಮೇಲೆ ಸೊನ್ನೆಯ ಬಲಭಾಗದಲ್ಲಿ ಧನ ಸಂಖ್ಯೆಗಳನ್ನು ಮತ್ತು ಎಡಭಾಗದಲ್ಲಿ ಋಣ ಸಂಖ್ಯೆಗಳನ್ನು ಬರೆಯುತ್ತೇವೆ.(ಇದನ್ನು ಪಾಠ 1.1 ರಲ್ಲಿ ಕಲಿತಿದ್ದೇವೆ.)
|
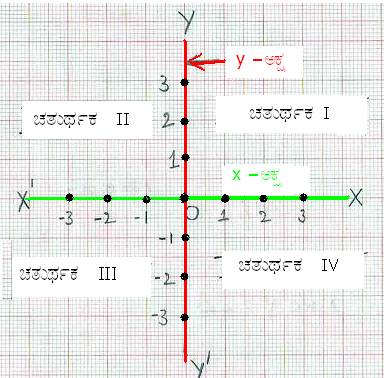
ನಕ್ಷಾಹಾಳೆ (ಗ್ರಾಫ್)ಯಲ್ಲಿ ಏಳೆದ ಒಂದು ಸರಳ ರೇಖೆಯನ್ನು ‘x – ಅಕ್ಷ’(‘x axis’. ) ಎನ್ನುತ್ತೇವೆ. ಆದ್ದರಿಂದ OX ರೇಖೆಯು ಧನ ಸಂಖ್ಯೆಗಳನ್ನು, OX1 ರೇಖೆಯು (ಇದನ್ನು -x ಎಂತಲೂ ಎನ್ನುತ್ತೇವೆ.) ಋಣ ಸಂಖ್ಯೆಗಳನ್ನು ಸೂಚಿಸುತ್ತದೆ. ಈಗ ‘O’ ಬಿಂದುವಿನಲ್ಲಿ x – ಅಕ್ಷಕ್ಕೆ ಬಿಂದು ಲಂಬವನ್ನೆಳೆದು ಅದನ್ನು ಕೆಳಗೂ ಮೇಲಕ್ಕೂ ವೃದ್ಧಿಸಿ. ಈ ಲಂಬ ರೇಖೆಯನ್ನು ‘y- ಅಕ್ಷ’(‘y axis’) ಎನ್ನುತ್ತೇವೆ.. x
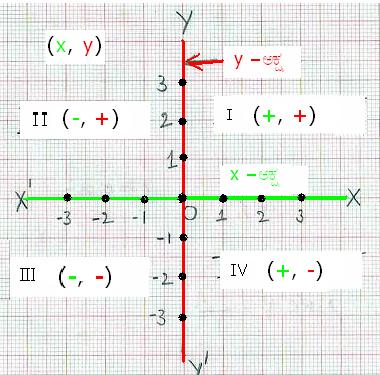
– ಅಕ್ಷ ದ ಮೇಲಿರುವ OY ರೇಖೆಯು ಧನ ಸಂಖ್ಯೆಗಳನ್ನು, ಕೆಳಗೆ ಇರುವ OY1 ರೇಖೆಯು ಋಣ ಸಂಖ್ಯೆಗಳನ್ನು ಸೂಚಿಸುತ್ತದೆ. ಈ x – ಅಕ್ಷ ಮತ್ತು y – ಅಕ್ಷ ಇವೆರಡನ್ನು ಒಟ್ಟಾಗಿ ‘ನಿರ್ದೇಶಾಂಕ ಅಕ್ಷಗಳು’( ‘coordinate axes’) ಎನ್ನುತ್ತೇವೆ. ಈ ನಿರ್ದೇಶಾಂಕ ಅಕ್ಷಗಳು ಸಮತಲವನ್ನು 4 ಭಾಗಗಳಾಗಿ ವಿಭಾಗಿಸುತ್ತವೆ. ಈ ಭಾಗಗಳಿಗೆ ಚತುರ್ಥಕಗಳು ಅಥವಾ ಪಾದಗಳು(‘quadrants’) ಎಂದು ಹೆಸರು. ಗಡಿಯಾರದ ಮುಳ್ಳಿನ ಚಲನೆಯ ವಿರುದ್ಧ (ಅಪ್ರದಕ್ಷಿಣ)ದಿಕ್ಕಿನಲ್ಲಿ ಈ ಚತುರ್ಥಕಗಳನ್ನು ಚತುರ್ಥಕ I, ಚತುರ್ಥಕ II, ಚತುರ್ಥಕ III, ಚತುರ್ಥಕ IV ಎಂದು ಕರೆಯುತ್ತೇವೆ. ನಕ್ಷಾಹಾಳೆಯಲ್ಲಿ x ಮತ್ತು y ಅಕ್ಷದ ಮೇಲೆ ಸಮದೂರದಲ್ಲಿ(1
ಸೆಂ.ಮೀ. ಆಗಿರಲಿ) O ಬಿಂದುವಿನ ಎರಡೂ ಬದಿಗಳಲ್ಲಿ ಗುರುತುಗಳಿವೆ. 1.
OX ನಲ್ಲಿ ಗುರುತುಗಳು O ಯಿಂದ ಬಲಕ್ಕೆ 1ಸೆಂ.ಮೀ., 2ಸೆಂ.ಮೀ., 3ಸೆಂ.ಮೀ.,. 2.
OX1 ನಲ್ಲಿ ಗುರುತುಗಳು O ಯಿಂದ ಎಡಕ್ಕೆ -1ಸೆಂ.ಮೀ., -2ಸೆಂ.ಮೀ.,-3 ಸೆಂ.ಮೀ. . .. 3.
OY ರೇಖೆಯಲ್ಲಿ O
ಯ ಮೇಲೆ 1ಸೆಂ.ಮೀ., 2ಸೆಂ.ಮೀ., 3ಸೆಂ.ಮೀ., …. 4.
OY1 ರೇಖೆಯಲ್ಲಿ O ಯ ಕೆಳಗೆ-1ಸೆಂ.ಮೀ., -2ಸೆಂ.ಮೀ., -3ಸೆಂ.ಮೀ. … |
|
ನಕ್ಷಾಹಾಳೆಯಲ್ಲಿ
ಬಿಂದುಗಳನ್ನು ಗುರುತಿಸುವುದು (Plotting
of points on a graph sheet)
|
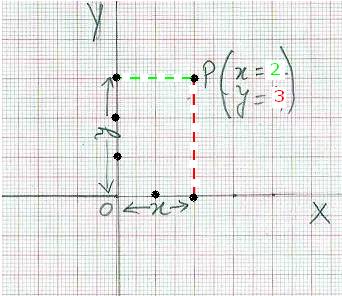
ಚತುರ್ಥಕ I ರಲ್ಲಿ (x –ಅಕ್ಷದಿಂದ ಮೇಲಕ್ಕೆ, y ಅಕ್ಷದಿಂದ ಬಲಕ್ಕೆ) ಯಾವುದೇ ಒಂದು ಬಿಂದು Pಯನ್ನು ಗುರುತಿಸಿ. P ಬಿಂದುವಿನಿಂದ x ಮತ್ತು y ಅಕ್ಷಗಳಿಗೆ ಸಮಾನಾಂತರ ರೇಖೆಗಳನ್ನೆಳೆಯಿರಿ. ಈ ರೇಖೆಗಳು X ಮತ್ತು Y ಅಕ್ಷಗಳನ್ನು ಸಂಧಿಸಿದಾಗ ಒಂದು ಆಯತ ದೊರೆಯುತ್ತದೆ. P ಯಿಂದ x ಅಕ್ಷಕ್ಕೆ ಎಳೆದ ಲಂಬವು ಅಕ್ಷವನ್ನು ಸಂಧಿಸುವ ಬಿಂದುವಿಗೆ ‘O’ ದಿಂದ ಇರುವ ದೂರವನ್ನು x - ನಿರ್ದೇಶಾಂಕ (‘x - coordinate’) ಅಥವಾ ಪ್ರಥಮ ಭುಜ (‘abscissa’) ಎನ್ನುವರು. P ಯಿಂದ x ಅಕ್ಷಕ್ಕೆ ಎಳೆದ ಸಮಾನಾಂತರ ರೇಖೆಯು y ಅಕ್ಷವನ್ನು ಸಂಧಿಸುವ ಬಿಂದುವಿಗೆ ‘O’ ದಿಂದ ಇರುವ ದೂರವನ್ನು y ನಿರ್ದೇಶಾಂಕ (‘y- coordinate’) ಅಥವಾ ನೀಳಭುಜ (‘ordinate ’) ಎನ್ನುವರು. ಪಕ್ಕದ ನಕ್ಷೆಯಲ್ಲಿ P ಬಿಂದುವಿನ x - ನಿರ್ದೇಶಾಂಕ 2 ಮಾನಗಳು(ಸೆಂ.ಮೀ.) ಮತ್ತು y-
ನಿರ್ದೇಶಾಂಕ 3
ಮಾನಗಳು (ಸೆಂ.ಮೀ.).ಆದ್ದರಿಂದ P
ಬಿಂದುವನ್ನು P(2,3) ಎಂದು ಬರೆಯುತ್ತೇವೆ. ಈ ನಿರ್ದೇಶಾಂಕಗಳನ್ನುಆಯತ ನಿರ್ದೇಶಾಂಕಗಳು (‘rectangular
coordinates’) ಎನ್ನುತ್ತೇವೆ. (ಏಕೆಂದರೆ ಆಕೃತಿ ಒಂದು ಆಯತವಾಗಿದೆ. |
|
7.1 ಸಮಸ್ಯೆ 1: ನಕ್ಷೆಯಲ್ಲಿ P(3, 2) ಬಿಂದು ಗುರುತಿಸಿ.
ಪರಿಹಾರ:
|
ಹಂತ 1: ನಕ್ಷಾಹಾಳೆಯಲ್ಲಿ x – ಅಕ್ಷದ ಮೇಲೆ, O ಬಿಂದುವಿನ 3 ಸೆಂ.ಮೀ. ದೂರದಲ್ಲಿ ಬಿಂದು (x1)
ಗುರುತಿಸಿ. ಹಂತ 2: ಅದೇರೀತಿ y – ಅಕ್ಷದ ಮೇಲೆ, O ಬಿಂದುವಿನಿಂದ 2 ಸೆಂ.ಮೀ. ದೂರದಲ್ಲಿ ಬಿಂದು (y1)
ಗುರುತಿಸಿ. ಹಂತ 3: Ox1
ಮತ್ತು Oy1 ಬಾಹುಗಳನ್ನಾಗಿ ಮಾಡಿ ಚತುರ್ಥಕ I ರಲ್ಲಿ ಒಂದು ಆಯತವನ್ನು ರಚಿಸಿ. Ox1
ಮತ್ತು Oy1
ಗಳಿಗೆ ಎಳೆದ ಸಮಾಂತರ ರೇಖೆಗಳು ಸಂಧಿಸುವ ಬಿಂದುವೇ P
(3, 2). ಅಭ್ಯಾಸ: T(2,
3) ಬಿಂದುವನ್ನು ನಕ್ಷೆಯಲ್ಲಿ ಗುರುತಿಸಿ. P
(3, 2), T (2, 3) ಗಳು ಬೇರೆಬೇರೆ ಬಿಂದುಗಳಾಗಿರುವುದನ್ನು ಗಮನಿಸಿ. ಯಾವುದೇ ಎರಡು ಬಿಂದುಗಳಿಗೆ ಒಂದೇ x ಮತ್ತು y ನಿರ್ದೇಶಾಂಕಗಳಿಲ್ಲ.ಆದ್ದರಿಂದ (x,
y) ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಅಣಿತಯುಗ್ಮ ಅಥವಾ ಕ್ರಮಯುಗ್ಮ ಎನ್ನುವರು. (‘ordered pair’) ಅಭ್ಯಾಸ: Q(-2,
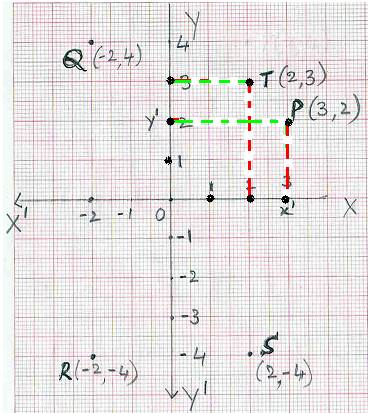
4), R(-2, -4), S(2, -4) ಈ ಬಿಂದುಗಳನ್ನು ನಕ್ಷೆಯಲ್ಲಿ ಗುರುತಿಸಿ. ಗಮನಿಸಿ: 1. ಋಣ x - ನಿರ್ದೇಶಾಂಕವನ್ನು x – ಅಕ್ಷದ ಮೇಲೆ O
ದಿಂದ ಎಡಕ್ಕೆ ಗುರುತಿಸುತ್ತೇವೆ.( (i.e. OX1 ರೇಖೆಯಲ್ಲಿ) 2. ಋಣ y - ನಿರ್ದೇಶಾಂಕವನ್ನು x – ಅಕ್ಷಕ್ಕಿಂತ ಕೆಳಗೆ OY1
ರೇಖೆಯ ಮೇಲೆ ಗುರುತಿಸುತ್ತೇವೆ. ಫಲಿತಾಂಶ: 1.
ಬಿಂದು Q (-2,
4) 2 ನೇ ಚತುರ್ಥಕದಲ್ಲಿದೆ. 2. ಬಿಂದು R (-2,
-4) 3
ನೇ ಚತುರ್ಥಕದಲ್ಲಿದೆ. 3.
ಬಿಂದು S (2,
-4) 4
ನೇ ಚತುರ್ಥಕದಲ್ಲಿದೆ. |
|
ಗಮನಿಸಿ:
|
1. ಮೂಲಬಿಂದು ‘O’ ನ ನಿರ್ದೇಶಾಂಕ: (0,
0). 2. x ಅಕ್ಷದ ಮೇಲಿನ ಯಾವುದೇ ಬಿಂದುವಿನ ನಿರ್ದೇಶಾಂಕ ( 3.
y ಅಕ್ಷದ ಮೇಲಿನ ಯಾವುದೇ ಬಿಂದುವಿನ ನಿರ್ದೇಶಾಂಕ (0,
|
|
7.1.1 ಸರಳ ಸಮೀಕರಣದ ನಕ್ಷೆ ಎಳೆಯುವುದು (Drawing
graph for a linear equation):
ಸರಳ ಸಮೀಕರಣಗಳು ಒಂದನೇ ಘಾತದ ಎರಡು ಚರಾಕ್ಷರಗಳನ್ನು ಹೊಂದಿದ ಸಮೀಕರಣಗಳು.
ಈಗ ನಾವು ಕೆಳಗೆ ಸೂಚಿಸಿದ ಸಂಬಂಧಗಳನ್ನು ನೋಡುವಾ, ಇವುಗಳಲ್ಲಿ ಒಂದು ಚರಾಕ್ಷರ x , ಇನ್ನೊಂದು y.
|
ಕ್ರ.ಸಂ. |
ಸಂಬಂಧ |
ಸಮಾನವಾದ ಸಮೀಕರಣ |
|
1 |
ಒಂದು ಸಂಖ್ಯೆಯು ಇನ್ನೊಂದು ಸಂಖ್ಯೆಗೆ ಸಮ. |
y
= x |
|
2 |
ಒಂದು ಸಂಖ್ಯೆಯು ಇನ್ನೊಂದರ ಎರಡರಷ್ಟಿದೆ. |
y
= 2x |
|
3 |
ಒಂದು ಸಂಖ್ಯೆಯು ಇನ್ನೊಂದರ ಎರಡರಷ್ಟಕ್ಕಿಂತ 1 ಹೆಚ್ಚು. |
y
= 2x+1 |
|
4 |
ಒಂದು ಸಂಖ್ಯೆಯು ಇನ್ನೊಂದು ಸಂಖ್ಯೆಗೆ 2
ನ್ನ ಕೂಡಿಸಿದುದರ 2 ರಷ್ಟಿದೆ. |
y
= 2(x+2) |
|
5 |
ಎರಡು ಸಂಖ್ಯೆಗಳ ವ್ಯತ್ಯಾಸ 3. |
x-y =3 or
–y = 3-x(ಸ್ಥಳಾಂತರಿಸಿದೆ.) ಅಥವಾ y = x-3(-1 ರಿಂದ ಗುಣಿಸಿದೆ) |
|
6 |
ಎರಡು ಸಂಖ್ಯೆಗಳ ಮೊತ್ತ =3 |
x+y=
3 ಅಥವಾ y = 3-x(ಸ್ಥಳಾಂತರಿಸಿದೆ.) |
ಮೇಲಿನ ಎಲ್ಲಾ ಸಮೀಕರಣಗಳು ಅವ್ಯಕ್ತ ಪದದ
ಮೊದಲನೇ ಘಾತದಲ್ಲಿವೆ. ಅವುಗಳ ಸಾಮಾನ್ಯರೂಪ y = mx + c . ಇಲ್ಲಿ c = ಒಂದು ಸ್ಧಿರಾಂಕ.
ಒಂದು ಸಮೀಕರಣವು ax+by+c
= 0 ರೂಪದಲ್ಲಿದ್ದರೂ ಅದನ್ನು y =mx+c ರೂಪಕ್ಕೆ
ಪರಿವರ್ತಿಸಬೇಕು. ಹೇಗೆ?
|
1 |
ax+by+c
= 0 |
ದತ್ತ |
|
2 |
by=
-ax-c |
ಸ್ಥಳಾಂತರಿಸಿದಾಗ(ಎರಡೂ ಕಡೆ ax+c ಯಿಂದ ಕಳೆದಾಗ) |
|
3 |
y=
(-a/b)x-(c/b) |
ಎರಡೂ ಕಡೆ b ಯಿಂದ ಭಾಗಿಸಿದಾಗ |
|
4 |
y
=mx+z |
m=
-(a/b), z= -(c/b) |
7.1.1 ಸಮಸ್ಯೆ
1: x+y =3 ಸಮೀಕರಣದ ನಕ್ಷೆ ಎಳೆಯಿರಿ.
ಪರಿಹಾರ:
|
ಹಂತ 1 : ದತ್ತ ಸಮೀಕರಣವನ್ನು y =mx+c ರೂಪಕ್ಕೆ ಪರಿವರ್ತಿಸಿ. (ಸಮೀಕರಣದ ಎಡಭಾಗದಲ್ಲಿ y ಮಾತ್ರ ಇರಬೇಕು.) y = 3-x(ಸ್ಥಳಾಂತರಿಸಿದೆ). ಹಂತ 2 : x
ನ ಕೆಲವು ಬೆಲೆಗಳಿಗೆ (ಬರೇ 2 ಬೆಲೆ ಸಾಕಾದರೂ ಸಹ) y ಯ ಬೆಲೆಗಳನ್ನು ಕಂಡು ಹಿಡಿದು ಕೆಳಗಿನಂತೆ ಪಟ್ಟಿಮಾಡಿ:
ಹಂತ 3
: ನಕ್ಷಾ ಹಾಳೆಯ ಮೇಲೆ (x,y) ನಿರ್ದೇಶಾಂಕಗಳಿರುವ ಬಿಂದುಗಳನ್ನು ಗುರುತಿಸಿ, ಒಂದು ಸರಳ ರೇಖೆಯಿಂದ ಈ ಬಿಂದುಗಳನ್ನು ಸೇರಿಸಿ. ಈ ಸರಳ ರೇಖೆಯು x+y
=3(ಅಥವಾ y=
-x +3) ಸಮೀಕರಣವನ್ನು ಸೂಚಿಸುತ್ತದೆ ತಾಳೆ:ನಮಗೆ ದೊರೆತ ಸರಳರೇಖೆಯು x+y=3
ಸಮೀಕರಣವನ್ನು ಸೂಚಿಸುತ್ತದೆ ಎಂಬ ಖಾತ್ರಿ ಹೇಗೆ? ನಮಗೆ ದೊರೆತ ರೇಖೆಯಲ್ಲಿ x=0.5
ಆದಾಗ y- ಯ ನಿರ್ದೇಶಾಂಕವನ್ನು ನೋಡಿ. ಅದು 2.5
ಆಗಿದೆ ಆ ಬಿಂದು (0.5,
2.5) ಆಗಿದೆ x,y ಗಳ ಈ ಬೆಲೆಗಳನ್ನು ದತ್ತ ಸಮೀಕರಣದಲ್ಲಿ ಆದೇಶಿಸಿದಾಗ,x+y
=0.5+2.5 = 3. ಇದೇ ರೀತಿ x ನ ಬೇರೆ ಬೆಲೆಗಳಿಗೂ ಸರಿ ಇದೆಯೇ { ಉದಾ: (3,0)} ಎಂದು ನೋಡುವುದರಿಂದ ಈ ರೇಖೆಯ ನಾವು ಎಳೆದ ನಕ್ಷೆಯು ದತ್ತ ಸಮೀಕರಣವನ್ನು ಸೂಚಿಸುತ್ತದೆ ಎಂದು ತಿಳಿಯಬಹುದು. y=
mx+c ಇದು ಮೊದಲ ಘಾತದ ಸಮೀಕರಣವಾಗಿದ್ದು ಎಳೆದ ನಕ್ಷೆಯು ಒಂದು ಸರಳರೇಖೆಯಾದ್ದರಿಂದ, ಇಂತಹ ಮೊದಲ ಘಾತದ ಸಮೀಕರಣಗಳನ್ನು ರೇಖಾತ್ಮಕ ಸಮೀಕರಣಗಳೆನ್ನುವರು.
(‘linear equations’) |
|
ಗಮನಿಸಿ:
1. ಒಂದು ಸರಳ ರೇಖೆಯನ್ನೆಳೆಯಲು
ಎರಡೇ ಬಿಂದುಗಳು ಸಾಕಾದರೂ ಕೂಡಾ x+y=3 ಸಮೀಕರಣಕ್ಕೆ ತುಂಬಾ ಪರಿಹಾರಗಳಿವೆಯೆಂದು ತೋರಿಸಲು (x,y)
ಗಳ ಹಲವು ಬೆಲೆಗಳನ್ನು ಪಟ್ಟಿಮಾಡಿದ್ದೇವೆ.
2. ನಕ್ಷೆಯ ಮೇಲಿನ ಹಲವು (
x,
y) ನಿರ್ದೇಶಾಂಕಗಳು x+y =3 ರೇಖೆಯ ಮೇಲೆ ಇದ್ದು { ಉದಾ.(4,-1)} ಇವೆಲ್ಲವೂ ದತ್ತ ಸಮೀಕರಣಕ್ಕೆ ಅನುಸಾರವಾಗಿವೆ.
ನಕ್ಷೆ ಎಳೆಯುವ ಪರ್ಯಾಯ ವಿಧಾನ
(Alternate Method
of drawing graph):
|
ಒಂದು ಸರಳ ರೇಖೆಯನ್ನೆಳೆಯಲು ನಮಗೆ ಬರೇ 2 ಬಿಂದುಗಳು ಸಾಕು. ಹಾಗಿದ್ದಲ್ಲಿ ನಾವು x,
y ಗಳಿಗೆ ಬೇರೆ ಬೇರೆ ಬೆಲೆಗಳ ಪಟ್ಟಿ ತಯಾರಿಸುವ ಅಗತ್ಯವೇನು? ನಿಜವಾಗಿ ನಮಗೆ ಬೇಕಾಗಿರುವುದು. x – ಅಕ್ಷದ ಮೇಲೆ ಒಂದು ಬಿಂದು, y – ಅಕ್ಷದ ಮೇಲೆ ಒಂದು ಬಿಂದು. ಈ ಎರಡು ಬಿಂದುಗಳನ್ನು ಸೇರಿಸಿ ನಾವು ಒಂದು ಸರಳ ರೇಖೆ ಯನ್ನೆಳೆಯಬಹುದು. x – ಅಕ್ಷದ ಮೇಲಿನ ಬಿಂದುವಿನ y – ಯ ನಿರ್ದೇಶಾಂಕ ಔ. ಅದೇರೀತಿ y – ಅಕ್ಷದ ಮೇಲಿನ ಬಿಂದುವಿನ x ನ ನಿರ್ದೇಶಾಂಕ =
O. ಒಂದು ರೇಖಾತ್ಮಕ ಸಮೀಕರಣದ ನಕ್ಷೆಯು x – ಅಕ್ಷವನ್ನು ಛೇದಿಸುವ ಬಿಂದುವನ್ನು x – ಅಂತಃಖಂಡ (‘x- intercept’) ಎನ್ನುತ್ತೇವೆ.
ಆ ಬಿಂದುವಿನ ನಿರ್ದೇಶಾಂಕಗಳು: (x,0). x ನ ಬೆಲೆ ಪಡೆಯಲು ದತ್ತ ಸಮೀಕರಣದಲ್ಲಿ y ಗೆ O ನ್ನು ಆದೇಶಿಸಿ. ಒಂದು ರೇಖಾತ್ಮಕ ಸಮೀಕರಣದ ನಕ್ಷೆಯು y
– ಅಕ್ಷವನ್ನು ಛೇದಿಸುವ ಬಿಂದುವಿನ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು y – ಅಂತಃಖಂಡ (‘y-
intercept’) ಎನ್ನುತ್ತೇವೆ. ಈ ಬಿಂದುವಿನ ನಿರ್ದೇಶಾಂಕಗಳು (0,y).
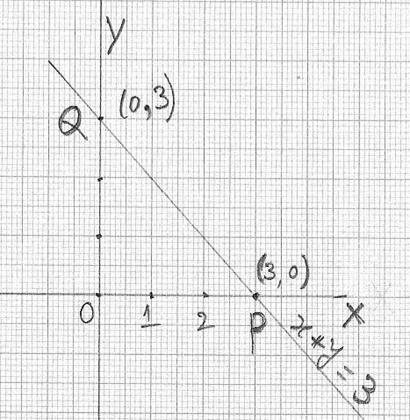
ಇಲ್ಲಿ y ಯ ಬೆಲೆಯನ್ನು ಪಡೆಯಲು ದತ್ತ ಸಮೀಕರಣದಲ್ಲಿ x=0 ಎಂದು ಆದೇಶಿಸಿ. ಈಗ ಈ ಪರ್ಯಾಯ ವಿಧಾನದಿಂದ x+y
= 3(ಸಮಸ್ಯೆ 2.7.1.1)
ಸಮೀಕರಣದ ನಕ್ಷೆ ಎಳೆಯುವಾ. ಸಮೀಕರಣದಲ್ಲಿ y=0 ಆದೇಶಿಸಿದಾಗ,x=3.
P(3,0) ಯು x- ಅಂತಃಖಂಡ. ಸಮೀಕರಣದಲ್ಲಿ x=0 ಆದೇಶಿಸಿದಾಗ, y=3. Q(0,3) ಯು y- ಅಂತಃಖಂಡ.P
ಮತ್ತು Q ಬಿಂದುಗಳನ್ನು ಸೇರಿಸುವಂತೆ ಸರಳರೇಖೆಯನ್ನೆಳೆದರೆ, x+y =3. ಸಮೀಕರಣದ ನಕ್ಷೆ ಸಿಗುತ್ತದೆ. ಇದು ಸಮಸ್ಯೆ 7.1.1.1
ರಲ್ಲಿದ್ದಂತೆಯೇ ಆಗಿದೆ. |
|
7.1.1 ಸಮಸ್ಯೆ 2: y = -2 ರ ನಕ್ಷೆ
ಎಳೆಯಿರಿ.
ಪರಿಹಾರ:
|
ಹಂತ
1: ಮೇಲ್ಕಂಡ ಸಮಸ್ಯೆಯನ್ನು ಹೀಗೂ ಅರ್ಥೈಸಬಹುದು; “x ನ ಯಾವ ಬೆಲೆಗೆ y =-2 ಆಗುತ್ತದೆ?” ಸಮೀಕರಣ ಬರೆಯುವುದಾದರೆ
ಹೀಗೆ ಬರೆಯಬಹುದು: y =0x-2 ಹಂತ 2: x ನ ಕೆಲವು ಬೆಲೆಗಳಿಗೆ y ಯ ಬೆಲೆಯನ್ನು ಲೆಕ್ಕ ಹಾಕಿ ಕೆಳಕಂಡಂತೆ ಪಟ್ಟಿಮಾಡಿ
ಹಂತ 3 : ನಕ್ಷಾ ಹಾಳೆಯ ಮೇಲೆ (x,
y) ನಿರ್ದೇಶಾಂಕಗಳಿಂದ ಸೂಚಿಸಿದ ಬಿಂದುಗಳನ್ನು ಗುರುತಿಸಿ, ಅವುಗಳನ್ನು ಸರಳರೇಖೆಯಿಂದ ಜೋಡಿಸಿ. ಈ ಸರಳರೇಖೆಯು y=-2 ನ್ನ ಸೂಚಿಸುತ್ತದೆ. ಈ ರೇಖೆಯ ಮೇಲೆ (2,-2) ಬಿಂದುವನ್ನು ಗಮನಿಸಿ. ಈ ಬಿಂದುವಿನ ನಿರ್ದೇಶಾಂಕಗಳು ದತ್ತ ಸಮೀಕರಣವನ್ನು ತೃಪ್ತಿ ಪಡಿಸುತ್ತವೆ. ಗಮನಿಸಿ:ಎಳೆದ ರೇಖೆಯು x – ಅಕ್ಷಕ್ಕೆ ಸಮಾಂತರವಾಗಿದೆ. |
|
7.1.1 ಸಮಸ್ಯೆ 3: 2y = -x
ಸಮೀಕರಣದ ನಕ್ಷೆ ಎಳೆ.
ಪರಿಹಾರ:
|
ಹಂತ 1: ಸಮೀಕರಣದ ಎಡಭಾಗದಲ್ಲಿ y ಮಾತ್ರವಿರುವಂತೆ ಸಮೀಕರಣವನ್ನು ಪರಿವರ್ತಿಸಿ: y = - x/2 ಹಂತ 2: x ನ 2 ಬೆಲೆಗಳಿಗೆ y ಯ ಬೆಲೆ ಕಂಡುಹಿಡಿ ಮತ್ತು ಪಟ್ಟಿಮಾಡಿ.
ಹಂತ 3: (x, y) ನಿರ್ದೇಶಾಂಕಗಳುಳ್ಳ ಈ ಎರಡು ಬಿಂದುಗಳನ್ನು ನಕ್ಷೆಯಲ್ಲಿ ಗುರುತಿಸಿ, ಸರಳ ರೇಖೆಯಿಂದ ಈ ಬಿಂದುಗಳನ್ನು ಜೋಡಿಸಿ. ದೊರೆತ ಸರಳ ರೇಖೆಯು y= -(1/2)x ಸಮೀಕರಣಕ್ಕನುಗುಣವಾಗಿದೆ. ಈ ಸರಳ ರೇಖೆಯ ಮೇಲಿನ ಬಿಂದು (1,-1/2) ವನ್ನು ಸಮೀಕರಣದಲ್ಲಿ ಆದೇಶಿಸಿ, ತಾಳೆನೋಡಿ. ಗಮನಿಸಿ: ಎಳೆದ ಸರಳರೇಖೆಯು ಮೂಲಬಿಂದು (0, 0). ಮೂಲಕ ಹಾದು ಹೋಗುತ್ತದೆ. |
|
7.1.1 ಸಮಸ್ಯೆ 4: x = -3 ರ ನಕ್ಷೆ ರಚಿಸಿ.
ಪರಿಹಾರ:
|
ಹಂತ 1: ದತ್ತ ಸಮೀಕರಣದ ಅರ್ಥ = y ಯ ಯಾವುದೇ ಬೆಲೆಗೆ x
= -3. ಈ ಕೆಳಗಿನಂತೆ ಪಟ್ಟಿಮಾಡಿ.
ಹಂತ
2: (x, y) ನಿರ್ದೇಶಾಂಕದಿಂದ ಸೂಚಿಸಿದ ಬಿಂದುಗಳನ್ನು ನಕ್ಷಾ ಹಾಳೆಯಲ್ಲಿ ಗುರುತಿಸಿ. ಎಲ್ಲಾ ಬಿಂದುಗಳನ್ನು ಸರಳರೇಖೆಯಿಂದ ಜೋಡಿಸಿ.ಈ ಸರಳರೇಖೆಯು x=-3
ನ್ನ ಸೂಚಿಸುತ್ತದೆ. ಗಮನಿಸಿ:ಎಳೆದ ಸರಳರೇಖೆಯು y
ಅಕ್ಷಕ್ಕೆ ಸಮಾಂತರವಾಗಿದೆ. |
|
7.1
ಕಲಿತ ಸಾರಾಂಶ
|
ಕ್ರ.ಸಂ.
|
ಕಲಿತ
ಮುಖ್ಯಾಂಶಗಳು |
|
1 |
x ಅಕ್ಷ ಮತ್ತು y ಅಕ್ಷಗಳನ್ನು ನಿರ್ದೇಶಾಂಕ ಅಕ್ಷಗಳೆನ್ನುವರು. |
|
2 |
ಯಾವುದೇ ಬಿಂದುವನ್ನು ಒಂದು ಅಣಿತಯುಗ್ಮ (x,y) ಯಿಂದ ಸೂಚಿಸುತ್ತೇವೆ ಮತ್ತು ಅದನ್ನು ಬಿಂದುವಿನ ನಿರ್ದೇಶಾಂಕಗಳೆನ್ನುತ್ತೇವೆ. |
|
3 |
ಮೂಲ ಬಿಂದುವಿನ ನಿರ್ದೇಶಾಂಕಗಳು (0,0) |
|
4 |
x – ಅಕ್ಷದ ಮೇಲಿನ ಯಾವುದೇ ಬಿಂದುವಿನ ನಿರ್ದೇಶಾಂಕ: (x,0) y – ಅಕ್ಷದ ಮೇಲಿನ ಯಾವುದೇ ಬಿಂದುವಿನ ನಿರ್ದೇಶಾಂಕ: (0,y) |
|
5 |
ನಕ್ಷೆಯಲ್ಲಿನ ಸರಳ ರೇಖೆಯ ಸಮೀಕರಣವು y = mx+c (ಮೊದಲನೇ ಘಾತದಲ್ಲಿರಬೇಕು) ರೂಪದಲ್ಲಿರುತ್ತದೆ ಮತ್ತು ನಕ್ಷೆಯನ್ನು ರೇಖಾತ್ಮಕ ನಕ್ಷೆ ಎನ್ನುವರು. |
|
6 |
x = ಸ್ಧಿರಾಂಶವಾದಾಗ ನಕ್ಷಾರೇಖೆ y ಅಕ್ಷಕ್ಕೆ ಸಮಾಂತರವಾಗಿರುವುದು. y = ಸ್ಧಿರಾಂಶವಾದಾಗ ನಕ್ಷಾರೇಖೆ x - ಅಕ್ಷಕ್ಕೆ ಸಮಾಂತರವಾಗಿರುವುದು. |
|
7 |
y = mx ಸಮೀಕರಣದ ನಕ್ಷೆ ಮೂಲಬಿಂದುವಿನ ಮೂಲಕ ಹಾದು ಹೋಗುತ್ತದೆ. |
|
8 |
ನಕ್ಷಾರೇಖೆಯು x- ಅಕ್ಷವನ್ನು ಛೇದಿಸುವ ಬಿಂದುವಿನ ನಿರ್ದೇಶಾಂಕವು, ಸಮೀಕರಣದ x- ಅಂತಃಖಂಡವಾಗಿರುತ್ತದೆ.(x,0) |
|
9 |
ನಕ್ಷಾರೇಖೆಯು y – ಅಕ್ಷವನ್ನು ಛೇದಿಸುವ ಬಿಂದುವಿನ ನಿರ್ದೇಶಾಂಕವು, ಸಮೀಕರಣದ y– ಅಂತಃಖಂಡವಾಗಿರುತ್ತದೆ.(0,y) |